Biosyn
- 114
- 0
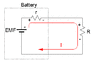
Homework Statement
A battery has an internal resistance of 0.50 ohm. A number of identical light bulbs, each with a resistance of 15 ohm, are connected in parallel across the battery terminals. The terminal voltage of the batter is observed to be one-half the EMF of the battery. How many bulbs are connected?
Homework Equations
V = Vemf - IR
The Attempt at a Solution
n = number of light bulbs
1/(Rb) = (1/15)n
Rb = 15/n
I'm not sure what to do at this point..
V = (1/2)Vemf