You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Is my Centroid Calculation Correct?
- Thread starter fonseh
- Start date
-
- Tags
- Calculation Centroid
AI Thread Summary
The discussion revolves around the calculation of the centroid for a specific shape and whether it aligns with the horizontal line of equal area. Participants confirm that symmetry supports the assertion that the centroid lies on the same horizontal line as the line of equal area. A discrepancy arises when one user calculates the plastic modulus (Zp) and arrives at a different answer than the provided solution, prompting questions about the method used. Clarifications suggest that the book's answer may refer to the elastic section modulus rather than the plastic section modulus. Ultimately, understanding the differences in these concepts is crucial for accurate calculations.
Physics news on Phys.org
Mark44
Mentor
- 38,043
- 10,530
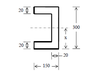
Do you mean "line of equal area"?fonseh said:Homework Statement
For this shape , it's clear that the centroid and the horizontal line of equal axis lies on the same horizontal line , am i right ?
Homework Equations
The Attempt at a Solution
I'm not sure . correct me if i am wrong . [/B]
Anyway, yes, symmetry should convince you that you're right if there's no other information given.
fonseh
- 521
- 2
Are you familiar with plastic analysis ? Zp here is the plastic modulus .Mark44 said:Do you mean "line of equal area"?
Anyway, yes, symmetry should convince you that you're right if there's no other information given.
I use another method to do , but i get different answer , why ?
Here's my working : , Zp = Sum of area x ( difference between centroid of particluar area and the equal area axis )
Zp = [ (130)(20)(150-10) + (150)(20)(150/2) ] x 2 = 1178000 , but the ans provided is only 929040
Mark44
Mentor
- 38,043
- 10,530
No, I'm not, but I am familiar with the concept of centroids.fonseh said:Are you familiar with plastic analysis ?
My answer is based on the fact that the shape in the drawing is symmetric about its horizontal midline.
fonseh said:Zp here is the plastic modulus .
I use another method to do , but i get different answer , why ?
Here's my working : , Zp = Sum of area x ( difference between centroid of particluar area and the equal area axis )
Zp = [ (130)(20)(150-10) + (150)(20)(150/2) ] x 2 = 1178000 , but the ans provided is only 929040
If you had a rectangular piece of some uniform, rigid material 150 mm by 300 mm, its centroid would be at the center of the piece, at a point 75 mm to the right of the left edge, and 150 mm above the lower edge. If you cut out a rectangle 130 mm by 260 mm to form a "C" shape as in your drawing, the centroid of the piece you remove would be at its center, and the centroid of the remaining C-shaped piece would be along the horizontal midline, but a bit right of where it was for the original uncut piece of material.
- 7,201
- 530
Your number looks correct for the plastic section modulus perhaps the book is looking for the elastic section modulus you'll have to run the numbers
My solution: v = 2*t + 5*t^2. dx/dt = 2*t + 5*t^2. Therefore dx = (2t + 5t^2)dt. After taking the anti derivative my equation is s = t^2/2 + 5/3(t^3).
Hi all,
I have a structural engineering book from 1979. I am trying to follow it as best as I can. I have come to a formula that calculates the rotations in radians at the rigid joint that requires an iterative procedure. This equation comes in the form of:
$$ x_i = \frac {Q_ih_i + Q_{i+1}h_{i+1}}{4K} + \frac {C}{K}x_{i-1} + \frac {C}{K}x_{i+1} $$
Where:
## Q ## is the horizontal storey shear
## h ## is the storey height
## K = (6G_i + C_i + C_{i+1}) ##
## G = \frac {I_g}{h} ##
## C...
Similar threads
- Replies
- 9
- Views
- 2K
- Replies
- 2
- Views
- 2K
Engineering
Center of gravity and stability of a system
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 19
- Views
- 4K
- Replies
- 1
- Views
- 3K
- Replies
- 4
- Views
- 2K
- Replies
- 1
- Views
- 10K
- Replies
- 4
- Views
- 1K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Engineering Diff gain of a push pull degenerated differential pair
- Started by arhzz
- Replies: 6
- Engineering and Comp Sci Homework Help
-
Engineering AGMA pitting resistance factor of safety (SH)
- Started by ironfalls18
- Replies: 2
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math