Kirchoff's Voltage Law: Circuit Troubleshooting Help

[goldfronts1]

I am having trouble with the attached circuit to find the voltage drops. Can anyone please assist. Thanks

 

[tiny-tim]

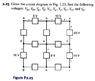
I am having trouble with the attached circuit to find the voltage drops. Can anyone please assist. Thanks

Hi goldfronts1!

Show us how far you've got, and where you're stuck, and then we'll know how to help.

 

[goldfronts1]

Ok I used the loops ad, be, dg, ef. All going clockwise from the node.

to get 4 equations and I set them equal to zero. however, from those four equations. you can't solve for any unknown variable. Please let me know if this is solvable as I have tried several different ways and can't come up with any solution.

Thanks

 

[tiny-tim]

Ok I used the loops ad, be, dg, ef. All going clockwise from the node.

to get 4 equations and I set them equal to zero. however, from those four equations. you can't solve for any unknown variable. Please let me know if this is solvable as I have tried several different ways and can't come up with any solution.

Hi goldfronts1!

Yes … there are only 4 independent equations, and 6 unknowns.

In fact, it's obvious that you can choose V_de and V_ef to be anything, and still solve for all the others.

Was there any other constraint … for example, all the resistances being equal?

 

[The Electrician]

It's strange that they would ask for the voltages, Vfa, Vac, Vai, and Vfb, since they can be determined without solving anything.

The remaining voltages can be found by traversing paths that don't pass through Vhg and Vih.

If you define 6 loop currents I1 through I6 in the loops as indicated, clockwise:

I1 = abed
I2 = bcfe
I3 = dehg
I4 = efih
I5 = abcfed
I6 = defihg

and create a 6x6 matrix to solve for the 6 unknown voltages, you will find that the matrix is rank deficient. The matrix has only rank 4, which means that two of the unknowns can be selected arbitrarily.

Designate a voltage by the symbol Vxy, which represents the voltage between nodes x and y, with node x being the positive end.

Let Vhg and Vih be selected arbitrarily; the we can solve for the other four:

Vda = Vhg+Vih+14
Veb = Vih+14
Ved = 8-Vhg
Vfe = -6-Vih

If you let Vhb = 0 and Vih =0, then:

Vda = 14
Veb = 14
Ved = 8
Vfe = -6

I hope I didn't make any mistakes, but you should check it out yourself.

 

[Defennder]

Yeah it looks like there are more unknowns than linearly independent loop equations can be constructed out of them. Odd. I always hated questions like these since it means you can't tell if you're doing something wrong.