etf
- 179
- 2
Hi!
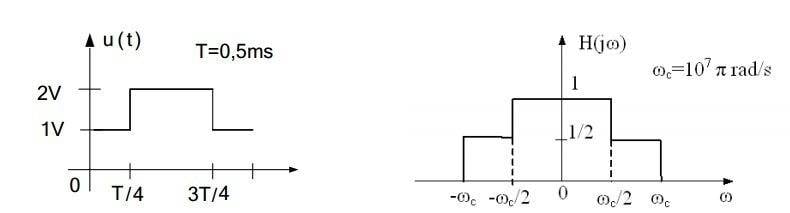
a) Calculate and sketch amplitude spectrum of u(t),
b) u(t) is input signal for linear time invariant system whose transfer function H(jw) is shown. Calculate output signal uo(t)
I completed task a), I got $$u(t)=\frac{3}{2}+\sum_{n=-\infty,n\neq 0}^{n=\infty}\frac{1}{2n\pi }(\sin{\frac{3n\pi}{2}}-\sin{\frac{n\pi}{2}})e^{jn\frac{2\pi}{0.5*10^{-3}}t},$$ where amplitude spectrum is $$F_n=|F_n|=\frac{1}{2n\pi }(\sin{\frac{3n\pi}{2}}-\sin{\frac{n\pi}{2}}).$$ Any suggestion about task b) ?
Homework Statement
a) Calculate and sketch amplitude spectrum of u(t),
b) u(t) is input signal for linear time invariant system whose transfer function H(jw) is shown. Calculate output signal uo(t)
Homework Equations
The Attempt at a Solution
I completed task a), I got $$u(t)=\frac{3}{2}+\sum_{n=-\infty,n\neq 0}^{n=\infty}\frac{1}{2n\pi }(\sin{\frac{3n\pi}{2}}-\sin{\frac{n\pi}{2}})e^{jn\frac{2\pi}{0.5*10^{-3}}t},$$ where amplitude spectrum is $$F_n=|F_n|=\frac{1}{2n\pi }(\sin{\frac{3n\pi}{2}}-\sin{\frac{n\pi}{2}}).$$ Any suggestion about task b) ?
Last edited: