c.teixeira
- 39
- 0
Hi there.
I am designing a type cilindrical can full of a fluid, with a temperature difference between the top and bottom. Now, after the simulation of the free convection phenomenom in COMSOL, I wanted to understand the effect of varying the temperatures, to the "fluid movement" (fluid flow/convection) that occurs within the can. To do so, I calculated the mass flow in the transverse plane ( the mid-plane[at the same distance from the top and bottom]): \dot{m} = \int\int\rho*w*dA.
The results I got for the mass flow were = 0. As there is no mass sink or source within the can, the mass flow had indeed to be zero unless it was compressing part of the liquid, and "creating" vacuum in another part of the can. So basically, the amount of mass that flows trough the mid-plane to the top is equal to the mass that flows trough the mid-plane to the bottom. However, what is relevant for my work, is to understand "how much liquid movement" occurs in the can. In order to do so, what do you think would be the most suitable surface integration I could use?
I tough about evaluating the following surface integral: \dot{m} = \int\int\rho*\sqrt{w^{2}}*dA.
In this case, the fluid crossing the plane of integration in direction to the bottom( with negative w) would count as positive mass flow. do you think this is a reasonable solution? do you have any sugestions?
Here is a sketch to make it more clear:
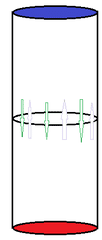
c.teixeira
I am designing a type cilindrical can full of a fluid, with a temperature difference between the top and bottom. Now, after the simulation of the free convection phenomenom in COMSOL, I wanted to understand the effect of varying the temperatures, to the "fluid movement" (fluid flow/convection) that occurs within the can. To do so, I calculated the mass flow in the transverse plane ( the mid-plane[at the same distance from the top and bottom]): \dot{m} = \int\int\rho*w*dA.
The results I got for the mass flow were = 0. As there is no mass sink or source within the can, the mass flow had indeed to be zero unless it was compressing part of the liquid, and "creating" vacuum in another part of the can. So basically, the amount of mass that flows trough the mid-plane to the top is equal to the mass that flows trough the mid-plane to the bottom. However, what is relevant for my work, is to understand "how much liquid movement" occurs in the can. In order to do so, what do you think would be the most suitable surface integration I could use?
I tough about evaluating the following surface integral: \dot{m} = \int\int\rho*\sqrt{w^{2}}*dA.
In this case, the fluid crossing the plane of integration in direction to the bottom( with negative w) would count as positive mass flow. do you think this is a reasonable solution? do you have any sugestions?
Here is a sketch to make it more clear:
c.teixeira