nickolaughagus
- 2
- 0
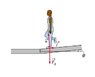
Look at the picture attached. There is a mass on a drawbridge, which is inclined at half a meter. We have the Normal force, the coefficient of static friction, force of gravity and the force of friction pushing the mass upwards to the end of the draw bridge that is most inclined. We also have \theta, from the joint of the bridge. Put the answer in terms of
What is the force of friction in terms of \theta and force of gravity, F_g
theta and force_gravityThe correct answer is Theta*F_g. How did they get this answer without any trig identities? Did it all cancel out?
What is the force of friction in terms of \theta and force of gravity, F_g
theta and force_gravityThe correct answer is Theta*F_g. How did they get this answer without any trig identities? Did it all cancel out?
Attachments
Last edited: