Sonya36
- 4
- 0
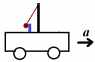
In class, we came up with an equation, a=gtanθ, to calculate the acceleration of a car using a hanging pendulum in Earth's frame of reference (θ being the angle that the pendulum makes with the vertical when the car accelerates). So far, I know that that the pendulum moves in the opposite direction of the car's acceleration and only tension force and gravity are acting on the pendulum in inertial frame of reference.
so eq1. Tsinθ=ma
eq2. Tcosθ=mg and when you solve for a, you get a=gtanθ
But we are trying to develop procedures for an experiment that verifies this equation. We need to find both acceleration and angle that the pendulum makes in an accelerating cart and prove that the equation is valid. We have a motion sensor to detect the acceleration of a moving cart. We are making the cart to accelerate at a constant rate by hanging a mass and dropping it. The part that we are not sure about is how to measure the angle that the pendulum makes with the vertical in the accelerating cart. We thought about taping a protractor to the cart and taking snapshots during the acceleration, but it's difficult to get a clear picture. Do you have any ideas or suggestions to improve our experiment?
so eq1. Tsinθ=ma
eq2. Tcosθ=mg and when you solve for a, you get a=gtanθ
But we are trying to develop procedures for an experiment that verifies this equation. We need to find both acceleration and angle that the pendulum makes in an accelerating cart and prove that the equation is valid. We have a motion sensor to detect the acceleration of a moving cart. We are making the cart to accelerate at a constant rate by hanging a mass and dropping it. The part that we are not sure about is how to measure the angle that the pendulum makes with the vertical in the accelerating cart. We thought about taping a protractor to the cart and taking snapshots during the acceleration, but it's difficult to get a clear picture. Do you have any ideas or suggestions to improve our experiment?