ksac
- 9
- 0
I am trying to get a hang of miller indices and doing some practice.
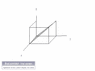
So here it is : What would be the miller indices of the plane containing the x-axis and equally inclined to y and z axes?
(I have uploaded the diagram and highlighted the plane to clarify)
Attempts :
I first try to find the intercepts.
The intercepts on the y and z axes are both, 0.
So does that make the corresponding miller indices k and l infinity? If yes, isn't the whole point of miller indices to avoid infinities in case of planes parallel to any of the crystal axes?
Also, what would be the intercept on the x axis, since the plane contains the x axis?
If there any gaps in my understanding or flaws in the way i am looking at it, please do correct me.
thank you :)
So here it is : What would be the miller indices of the plane containing the x-axis and equally inclined to y and z axes?
(I have uploaded the diagram and highlighted the plane to clarify)
Attempts :
I first try to find the intercepts.
The intercepts on the y and z axes are both, 0.
So does that make the corresponding miller indices k and l infinity? If yes, isn't the whole point of miller indices to avoid infinities in case of planes parallel to any of the crystal axes?
Also, what would be the intercept on the x axis, since the plane contains the x axis?
If there any gaps in my understanding or flaws in the way i am looking at it, please do correct me.
thank you :)