I Multiple integral Jacobian confusion

[Beelzedad]

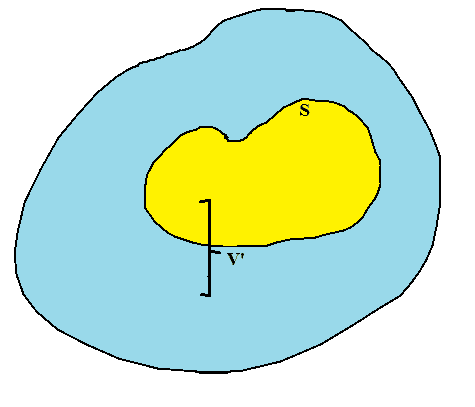
Consider a continuous charge distribution in volume $V'$. Draw a closed surface $S$ inside the volume $V'$.

___________________________________________________________________________

Consider the following multiple integral:
$\displaystyle B= \iint_S \Biggl( \iiint_{V'} \left[ \dfrac{\cos(\hat{R},\hat{n})}{R^2} \rho'\ \right] dV' \Biggl) dS \tag1$
where
$R=|\mathbf{r}-\mathbf{r'}|$
$\mathbf{r'}=(x',y',z')$ is coordinates of source points
$\mathbf{r}=(x,y,z)$ is coordinates of field points
$\cos(\hat{R},\hat{n})$ is the angle between $R$ and normal to surface element
$\rho'$ is the charge density and is continuous throughout the volume $V'$
__________________________________________________________________________
When $\mathbf{r} \in S$, the function is not integrable in domain $V'$. So we use change of variables:
$\displaystyle B= \iint_S \Biggl( \iiint_{V'} \left[ \dfrac{\cos(\hat{R},\hat{n})}{R^2} \rho'\ {r'}^2 \sin \theta' \right] d\theta' d\phi' dr' \Biggr) dS \tag2$
Note that in this equation, $\theta'$ and $\phi'$ are w.r.t point $\mathbf{r} \in S$
__________________________________________________________________________

Now by changing the order of integration:

$\displaystyle B = \iiint_{V'} \Biggl( \iint_S \left[ \dfrac{\cos(\hat{R},\hat{n})}{R^2} \rho'\ {r'}^2 \sin \theta' \right] dS \Biggr) d\theta' d\phi' dr' \tag3$
$\displaystyle B= \iiint_{V'} \Biggl( \iint_S \left[ \dfrac{\cos(\hat{R},\hat{n})}{R^2} \right] dS \Biggr) \rho'\ {r'}^2 \sin \theta' d\theta' d\phi' dr' \tag4$

Now here is my question:

Here in this last equation, $\theta'$ and $\phi'$ are w.r.t. which point?

[1]: https://i.stack.imgur.com/mz1VV.png

 

[jedishrfu]

It has to be the same origin point from the x,y,z system you transformed from, right?

When you transform from x,y,z to spherical coordinates, the angles are with respect to the origin unless you do some kind of translation to a new origin.

Calling @fresh_42 or @Mark44 for confirmation.

 

[Beelzedad]

It has to be the same origin point from the x,y,z system you transformed from, right?

When you transform from x,y,z to spherical coordinates, the angles are with respect to the origin unless you do some kind of translation to a new origin.

Calling @fresh_42 or @Mark44 for confirmation.

While computing the surface integral in my first equation, each point $\in S$ are origins. (There are infinitely many origins and infinitely many transformations from Cartesian to spherical). But in my last integral there must only be one spherical coordinate system. This is the problem.

 

[jedishrfu]

So does this mean in trying to change the order of integration you did something you can't do or that you didn't adjust the limits as well?

Perhaps if you go back to the meaning of the dS element you'll see your error.

 

[Beelzedad]

So does this mean in trying to change the order of integration you did something you can't do or that you didn't adjust the limits as well?

(1) I don't think I did something which is mathematically illegal. Am I correct?

(2) I am not talking about a particular volume and surface. The volume could be any volume and the surface could be any surface (provided that the whole surface is contained within the volume). Thus the limits are arbitrary.

 

[jedishrfu]

When the volume integral is evaluated you'll get a function in terms of r, theta and phi or a number if there are limits for these variables.

Then you are dotting the dS with that volume function.

I'm trying to work through this complexity myself.

There's a discussion in the wiki article on advanced stuff which may have some bearing on your problem:

https://en.wikipedia.org/wiki/Surface_integral

Advanced issues[edit]
Let us notice that we defined the surface integral by using a parametrization of the surface S. We know that a given surface might have several parametrizations. For example, if we move the locations of the North Pole and the South Pole on a sphere, the latitude and longitude change for all the points on the sphere. A natural question is then whether the definition of the surface integral depends on the chosen parametrization. For integrals of scalar fields, the answer to this question is simple, the value of the surface integral will be the same no matter what parametrization one uses.

For integrals of vector fields, things are more complicated, because the surface normal is involved. It can be proven that given two parametrizations of the same surface, whose surface normals point in the same direction, one obtains the same value for the surface integral with both parametrizations. If, however, the normals for these parametrizations point in opposite directions, the value of the surface integral obtained using one parametrization is the negative of the one obtained via the other parametrization. It follows that given a surface, we do not need to stick to any unique parametrization; but, when integrating vector fields, we do need to decide in advance which direction the normal will point to and then choose any parametrization consistent with that direction.

Another issue is that sometimes surfaces do not have parametrizations which cover the whole surface. The obvious solution is then to split that surface into several pieces, calculate the surface integral on each piece, and then add them all up. This is indeed how things work, but when integrating vector fields, one needs to again be careful how to choose the normal-pointing vector for each piece of the surface, so that when the pieces are put back together, the results are consistent. For the cylinder, this means that if we decide that for the side region the normal will point out of the body, then for the top and bottom circular parts the normal must point out of the body too.

Lastly, there are surfaces which do not admit a surface normal at each point with consistent results (for example, the Möbius strip). If such a surface is split into pieces, on each piece a parametrization and corresponding surface normal is chosen, and the pieces are put back together, we will find that the normal vectors coming from different pieces cannot be reconciled. This means that at some junction between two pieces we will have normal vectors pointing in opposite directions. Such a surface is called non-orientable, and on this kind of surface, one cannot talk about integrating vector fields

 

[Beelzedad]

When the volume integral is evaluated you'll get a function in terms of r, theta and phi or a number if there are limits for these variables.

Then you are dotting the dS with that volume function.

I'm trying to work through this complexity myself.

There's a discussion in the wiki article on advanced stuff which may have some bearing on your problem:

https://en.wikipedia.org/wiki/Surface_integral

I think I ran into another problem now. Please have a look at my equation labeling of post #1.

In equation (2), while computing the volume integral in spherical coordinates (here $\mathbf{r'}$ varies and $\mathbf{r}$ is constant), we take the origin of our spherical coordinate at point $\mathbf{r} \in S$. That is, $\mathbf{r}=(0,0,0)$

Therefore in equation (2), after computing (i.e. after applying the limits) the volume integral in spherical coordinates, we will definitely get a number and NOT a function of $(r,\theta,\phi)$ or $(x,y,z)$. Then how can I compute the surface integral?

 

[Beelzedad]

I think equation (2) as a whole is not iterated integral. The volume integral can be found by iterated integrals. We have to find the volume integral for all points $\mathbf{r} \in S$ and then do the surface integral (I don't know how, maybe by numerical integration).

If this is what is really going on in equation (2), is it valid to swap the order of surface and volume integral?