Magnetosphere
- 64
- 5
Homework Statement
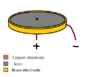
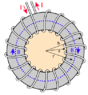
A DC current is flowing between two electrodes through a iron disk medium. Positive is attached to the copper shaft of the disc and the negative is attached to the outer brass periphery of the disk. The radius of the disk is 2,54mm (1 inch) and the height of the disk is 1cm. How does the magnetic field look/behave when a DC current is applied to the disk?
Homework Equations
Right hand rule
The Attempt at a Solution
I have searched online for the answer and made a few attempts at figuring it out myself but without any success. I can´t wrap my head around it.