Serbiwni
- 2
- 0
- Homework Statement
- Carl tries to move a table, which has a pile of books sitting on it of total mass m_books. The dynamic coefficient of friction is μd (between the table and floor) and the static coefficient of friction between the table and books is μs . Determine the maximum force that Carl can apply to the table so that the books do not slide.
Assume the books do not slide with respect to each other.
Numerical application: μs = 0.75, μd = 0.5, m_books = 3 kg, m_table = 10 kg
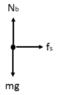
1) Draw the free body diagram of the books.
- Relevant Equations
- .
I drew a free body diagram for the books but it's not the same one in the correction. The static force Fs between the books and the table must be opposite to the motion but the correction does not the same and puts that vector in the same direction as the motion. Here's a drawing of the situation and also the free body diagram of the correction, as you can see its direction is also the motion's one.