Sentience
- 77
- 0
Homework Statement
http://rwdacad01.slcc.edu/academics/dept/physics/tvanausdal/2210/problems/force/force3.htm
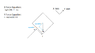
A block is given a push up the incline so it has an initial velocity of 5 m/s up the incline. If the incline angle is 30 degrees and the coefficient of kinetic friction is 0.2, what will be the stopping distance of the block?
Homework Equations
F = m * a
Force of friction = mu * Fn
The Attempt at a Solution
I do just fine until I go to set up the equation for the forces acting in the x direction. When this block is pushed it will move up the incline a bit, then come back down the incline because of friction and gravity. Both of these forces are pointing down in the incline right?
If you click on the solution, my instructor has it set up so both forces are negative. It just seems like going to the right would be the positive x direction.
Could I instead write it out so both are positive?
I feel like I understand everything in these problems just fine, I just set get the sign on one of my components wrong. (usually gravity acting in the horizontal direction) Do you have a foolproof way of setting them up consistently so your signs aren't off?
Last edited by a moderator: