Newton's Laws of motion -- Bicyclist pedaling up a slope

[paulimerci]

Homework Statement

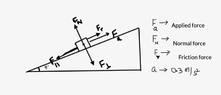
A 65 kg cyclist on a 10 kg bicycle is moving uphill on a 9° slope. How much force does he provide
if the bicycle slows at a rate of 0.3 m/s2?

Relevant Equations

Net force = ma

F parallel - F applied - rolling resistance = ma
I don't know how to calculate for rolling resistance. If the bicycle is not slipping rather it is rolling, should I ignore rolling resistance? And if I ignore that I would get,
F parallel - F applied = ma
F applied = F parallel -ma
= mg sin theta -ma
= 75x0.3 - 75 x 9.8 x sin9
= 92.5N
And the answer I got is not correct. Looks like mass is taken as 65kg and not as combined mass 75kg and I don't know why?

 

[Orodruin]

The question is badly posed. What does ”force he provides” mean?

However, the interpretation that gives the sought answer is what the net force of the bicyclist on the bike is.

 

[haruspex]

I don't know how to calculate for rolling resistance

It is not specified, so take it as zero.

75x0.3 - 75 x 9.8 x sin9

It's 65, not 75. And you have reversed the sign; in the preceding line you had mg sin theta -ma

 

[paulimerci]

Thank you, why 65 is used rather than 75?

 

[Orodruin]

Thank you, why 65 is used rather than 75?

the interpretation that gives the sought answer is what the net force of the bicyclist on the bike is.

 

[paulimerci]

The question is badly posed. What does ”force he provides” mean?

However, the interpretation that gives the sought answer is what the net force of the bicyclist on the bike is.

oh okay, Now I got it. Thank you!

 

[Orodruin]

oh okay, Now I got it. Thank you!

So, for posterity, can you give the full correct argument?

 

[PeroK]

So, for posterity, can you give the full correct argument?

In answering this question the student ought to think more deeply on how a bicycle works. The questions that spring to mind are:

1) How can the force be independent of the mass of the bicycle? What if the bicycle had a $100 kg$ trailer attached?

2) What is the force on the bicycle from the ground? Explain that!

3) If the cyclist dismounted and pushed the bike up the hill at constant speed, then this would require a greater force. Explain that!

In other words, simply solving the required force equation is only the tip of the iceberg in terms of understanding the mechanics of cycling uphill.

 

[erobz]

1) How can the force be independent of the mass of the bicycle? What if the bicycle had a $100 kg$ trailer attached?

I solved it by just considering the rider as the free body. You see very quickly in that approach the force applied to the bike is independent of the bikes mass, and or rolling resistance. But an intuitive explanation for this is escaping me.

 

[Orodruin]

I solved it by just considering the rider as the free body. You see very quickly in that approach the force applied to the bike is independent of the bikes mass, and or rolling resistance. But an intuitive explanation for this is escaping me.

How do you see this? What is your argumentation? What forces act on the rider? How does this relate to the force of the rider on the bike?

 

[erobz]

How do you see this? What is your argumentation? What forces act on the rider? How does this relate to the force of the rider on the bike?

This can't be good...many frantic questions.

I see a force of static friction acting on the on soles of the rider's feet, and whatever reaction is at the handlebars. The net force $-f_{app}$ that the rider is applying to the bike parallel to the slope are opposite the parallel components being applied to the rider from the bike by Newtons Third

Let $M$ be the mass of the rider:

$$ \nearrow^+ \sum F = f_{app} - M g \sin \theta = M(-a) \implies f_{app} = M(g \sin \theta - a ) $$

How many things don't I understand?

 

[PeroK]

I solved it by just considering the rider as the free body. You see very quickly in that approach the force applied to the bike is independent of the bikes mass, and or rolling resistance. But an intuitive explanation for this is escaping me.

You perhaps need to think about the mechanics of a bicycle and its gearing mechanism.

 

[erobz]

You perhaps need to think about the mechanics of a bicycle and its gearing mechanism.

I don't know if I'm following. It seems like the net force we can apply to the bike is proportional to our weight ( proportionality < 1)

 

[PeroK]

I don't know if I'm following. It seems like the net force we can apply to the bike is proportional to our weight ( proportionality < 1)

It's not your homework, so perhaps let the OP come back on this?

Not to give too much away, there must be a larger force from the ground on the back wheel of the bicycle. If you were walking with the bike, you would be pushing it forward. When you are cycling you are pushing the bike backwards - opposite to the direction it needs to go!

 

[erobz]

It's not your homework, so perhaps let the OP come back on this?

Not to give too much away, there must be a larger force from the ground on the back wheel of the bicycle. If you were walking with the bike, you would be pushing it forward. When you are cycling you are pushing the bike backwards - opposite to the direction it needs to go!

Fair enough, I'll wait for further exploration. This is quite interesting (IMO).[EDIT]
However, it's been my experience that when a student solves the problem, that's usually good enough. They have 90 others to solve in multiple courses and don't have time to explore "extra problems" in detail. We'll see.

 

[haruspex]

the interpretation that gives the sought answer is what the net force of the bicyclist on the bike is.

… if we ignore the component normal to the slope?

 

[erobz]

… if we ignore the component normal to the slope?

What can we conclude about the component of the applied force normal to the surface? As far as I can see if we are assuming the riders center of mass is not accelerating in a direction normal to the surface, it must be $Mg \cos \theta$?

 

[kuruman]

… if we ignore the component normal to the slope?

That's a good question. My answer to that would be "yes" because I agree with the solution proposed by @erobz which is the net force exerted by the bike in the direction of motion. The problem asks "How much force does he provide $\dots$ If the bike were at rest with the cyclist just sitting on it (no rolling, no sliding), is it sensible to say that the cyclist "provides" force $mg$ to the bike? I think the word "provides" muddles the issue.

 

[Orodruin]

If the bike were at rest with the cyclist just sitting on it (no rolling, no sliding), is it sensible to say that the cyclist "provides" force $mg$ to the bike? I think the word "provides" muddles the issue.

This is why I dislike the question formulation. It is not very precise.

 

[haruspex]

That's a good question. My answer to that would be "yes" because I agree with the solution proposed by @erobz which is the net force exerted by the bike in the direction of motion. The problem asks "How much force does he provide $\dots$ If the bike were at rest with the cyclist just sitting on it (no rolling, no sliding), is it sensible to say that the cyclist "provides" force $mg$ to the bike? I think the word "provides" muddles the issue.

But you cannot have it both ways. If you think it means extra force, compared with staying still, you have to leave out the vertical mg, not just the component normal to the slope.
The only way I see to fix it is that the question should specify parallel to the slope. And yes, "exerts on" would be better than "provides".

 

[paulimerci]

It's not your homework, so perhaps let the OP come back on this?

Not to give too much away, there must be a larger force from the ground on the back wheel of the bicycle. If you were walking with the bike, you would be pushing it forward. When you are cycling you are pushing the bike backwards - opposite to the direction it needs to go!

Thank you for counting on me! When the bicyclist starts to petal, the rear of the wheel pushes the bicycle backwards as it moves forward, and the direction of rolling friction changes as the bicycle advances. This friction pushes the bike to move forward. The rolling friction is assumed to be zero in this situation, although it is not. Am I correct? What will the front wheel's rolling resistance be. Does it experience rolling resistance in the same plane as the back end?

 

[PeroK]

Thank you for counting on me! When the bicyclist starts to petal, the rear of the wheel pushes the bicycle backwards as it moves forward, and the direction of rolling friction changes as the bicycle advances. This friction pushes the bike to move forward. The rolling friction is assumed to be zero in this situation, although it is not. Am I correct? What will the front wheel's rolling resistance be. Does it experience rolling resistance in the same plane as the back end?

It may not be worth your while spending too much time worrying about this problem. The issue isn't rolling friction. We can assume that resisting forces (other than gravity) are negligible here.

After some thought, I think that the problem is not just badly phrased but wrong. There's no doubt about the net force on the cyclist. But, that's not necessarily related to any active force that the cyclist provides. Here's my analysis.

Let's consider a modern bicycle where the rider is seated and manifestly pushes forward on the pedals with force $F_1$. There is then an equal and opposite reaction force from the pedals.

There is also a force from the seat of the bicycle forward on the rider ($F_2$) and an equal and opposite reaction from the rider's back. The unbalanced force is $F_2 - F_1$ and this is what accelerates the rider and what has been calculated here. Whereas, by no stretch of the imagination is that the force that the rider provides. The rider provides the force $F_1$. And, clearly, this force depends on the gearing mechanism of the bicycle. And, if you ride a mountain bike, you see how much that force ($F_1$) can vary across the gears.

You might argue that the rider is ultimately responsible for the net force $F_2 - F_1$, but there is also a third force ($F_3$) from the ground to the bicycle. And, ultimately, the rider is responsible for that force as well.

You might also argue that $F_2 - F_1$ is the net force provided by the rider to the bicycle. And that "provides" includes passive, reaction forces. But, then, the same argument would apply to a motorist being accelerated by a car seat. There is an equal and opposite force provided by the motorist's back on the car. So, you would have to say that the motorist is "providing" the force in that case too.

 

[jbriggs444]

After some thought, I think that the problem is not just badly phrased but wrong. There's no doubt about the net force on the cyclist. But, that's not necessarily related to any active force that the cyclist provides. Here's my analysis.

I would phrase it somewhat differently. There is an average net force of cyclist on bicycle. Naturally there is an equal and opposite net force of bicycle on cyclist. This net force is the sum of any number of individual interactions between cyclist and bicycle. Hands on handlebars (right and left), feet on pedals (right and left), posterior on seat. Some of these interfaces (notably the pedals) are in motion. Work is being done across those interfaces.

We are in a position to know their sum -- the average net force. But we are in a position to know one more summary fact about them. We can add up the rate at which work is being done across each of these interfaces and obtain a figure for work. Or average net power flowing from cyclist to bicycle.

[Average net power is not an invariant quantity. For the scenario at hand, I would probably adopt the rest frame of the cyclist+cycle to evaluate average net power, thus avoiding any contribution from the non-zero net force between them]

If we want to balance the momentum books, then average net force is the appropriate figure.
If we want to balance the energy books, then average net power is the figure to look at.

Speaking about the net force between cyclist and bicycle as if that were the single relevant interaction or even the most important interaction between them suggests a disappointing lack of insight on the part of the question writer. In real life, it is about how hard you pedal, not how hard you sit.

 

[erobz]

I don't know if I'm following. It seems like the net force we can apply to the bike is proportional to our weight ( proportionality < 1)

Looking at this a little closer I retract this statement. You certainly can apply a force to the pedals greater than your weight (as long as you can pull on the handlebars and have ample traction at the rear wheels). I believe the force you can apply would be limited by (other than your personal strength) the sum of the torques about the point of contact on the rear tire, such that the front tire normal force goes to zero. Also, the acceleration of the rider's center of mass vertically to apply the force would limit it over the pedal stroke.

I don't know if this is "good", but it has to be better than what I was thinking before.

 

[Lnewqban]

Looking at this a little closer I retract this statement. You certainly can apply a force to the pedals greater than your weight (as long as you can pull on the handlebars).

That makes all the forces of the mechanism (bicycle-muscles) internal; therefore, I believe the whole mass of 75 kg should be considered in the problem.

Rather than considering the instantaneous force on a pivot of the mechanism (foot-pedal), I would calculate the force that the contact patch applies rearward and in a direction parallel to the slope of 9°.

The mass of bike plus rider is propelled forward by the reactive force on the axle of the rear tire (equal in magnitude and in opposite direction to the force on the contact patch).

That human generated force is evidently not as big as the force generated by gravity rearward and in a direction parallel to the slope, as the movement is steadily slowing down.

That rate of negative acceleration should be proportional to the net force in a direction parallel to the slope and to the mass of bike plus rider.

 

[erobz]

That makes all the forces of the mechanism (bicycle-muscles) internal; therefore, I believe the whole mass of 75 kg should be considered in the problem.

Rather than considering the instantaneous force on a pivot of the mechanism (foot-pedal), I would calculate the force that the contact patch applies rearward and in a direction parallel to the slope of 9°.

The mass of bike plus rider is propelled forward by the reactive force on the axle of the rear tire (equal in magnitude and in opposite direction to the force on the contact patch).

That human generated force is evidently not as big as the force generated by gravity rearward and in a direction parallel to the slope, as the movement is steadily slowing down.

That rate of negative acceleration should be proportional to the net force in a direction parallel to the slope and to the mass of bike plus rider.

I was just saying that as a general statement about the mechanics of pedaling a bike. Not in regard to this specific problem.

 

[Lnewqban]

I was just saying that as a general statement about the mechanics of pedaling a bike. Not in regard to this specific problem.

I agreed with you then and I agree now.
In my view, not much different than using and engine or an electrical motor to propel a bicycle uphill, except the less homogeneous supplied output torque from legs.

 

[Orodruin]

That makes all the forces of the mechanism (bicycle-muscles) internal; therefore, I believe the whole mass of 75 kg should be considered in the problem.

But the problem in essence asks about the force on the rider — not rider+bike.

as long as you can pull on the handlebars and have ample traction at the rear wheels

You do not need to pull the handlebars. Even if the pedals were the only point of contact, the instantaneous force on the pedals can very well be larger than the weight. It just requires the biker to accelerate up.

 

[jbriggs444]

Even if the pedals were the only point of contact, the instantaneous force on the pedals can very well be larger than the weight. It just requires the biker to accelerate up.

Absent toe clips or a firm grip on the handlebars, it is difficult to achieve an average downforce on the pedals in excess of the person's weight. Acceleration can help with peak force. Not so much with average.

Well, maybe if one is cycling in the globe of death.

 

[erobz]

You do not need to pull the handlebars. Even if the pedals were the only point of contact, the instantaneous force on the pedals can very well be larger than the weight. It just requires the biker to accelerate up.

Ok, I can see that as possible. Imagine a riding without hands in a sitting position and standing up during the downward pedal stoke. It's very difficult to do in practice...I've tried it.

 

[haruspex]

it has to be better than what I was thinking before.

No, it just adds irrelevant details. The question asks for one force; it can only mean net force. Breaking it into all the different forces / torques exerted on pedals, handlebars and saddle just confuses the picture.
Likewise, it is not that important whether the acceleration specified is instantaneous, constant or average; whichever adjective applies to that applies to the force.
As you originally wrote, net force on cyclist $=m\vec a$.
Force bicycle exerts on cyclist $= m(\vec a-\vec g)$.
Force cyclist exerts on bicycle $= m(\vec g-\vec a)$.
The flaw in the question is that to get the given answer it should ask for the component parallel to the plane.

 

[erobz]

No, it just adds irrelevant details. The question asks for one force; it can only mean net force. Breaking it into all the different forces / torques exerted on pedals, handlebars and saddle just confuses the picture.
Likewise, it is not that important whether the acceleration specified is instantaneous, constant or average; whichever adjective applies to that applies to the force.
As you originally wrote, net force on cyclist $=m\vec a$.
Force bicycle exerts on cyclist $= m(\vec a-\vec g)$.
Force cyclist exerts on bicycle $= m(\vec g-\vec a)$.
The flaw in the question is that to get the given answer it should ask for the component parallel to the plane.

I'm sorry for the confusion. Those were just general thoughts on the mechanics of pedaling a bike (exploration for the sake of amusement). They weren't supposed to be specifically applied to solve this problem.

 

[Orodruin]

Ok, I can see that as possible. Imagine a riding without hands in a sitting position and standing up during the downward pedal stoke. It's very difficult to do in practice...I've tried it.

I did not say it would be advisable. It was merely a theoretical statement regarding the possible size of the pedal force.

 

[Orodruin]

Absent toe clips or a firm grip on the handlebars, it is difficult to achieve an average downforce on the pedals in excess of the person's weight. Acceleration can help with peak force. Not so much with average.

Well, maybe if one is cycling in the globe of death.

Which is why I had carefully added the word ”instantaneous” …

Edit: When attending a conference in Beijing some 9 years ago or so I also visited an acrobat show. The globe of death act was great. 8 motorcycles in the globe at the same time.

 

[Lnewqban]

Force bicycle exerts on cyclist $= m(\vec a-\vec g)$.
Force cyclist exerts on bicycle $= m(\vec g-\vec a)$.
The flaw in the question is that to get the given answer it should ask for the component parallel to the plane.

But the problem in essence asks about the force on the rider — not rider+bike.

But the bicyclist can’t push the pedal downwards and the bike uphill without having the bike pushing his mass along, so he stays on the pedal during the slowdown process.

Want it or not, his energy or work is accelerating the mass of the bike and his own mass simultaneously, while gravity is doing the opposite work, ...and winning.

Where is our expert mountan biker @berkeman when we need him?