- #1
etf
- 179
- 2
Hi!
Here is my task:
OPAMP circuit and output voltag are shown in image below. Assuming that OPAMP is ideal, come up with a solution by hand.
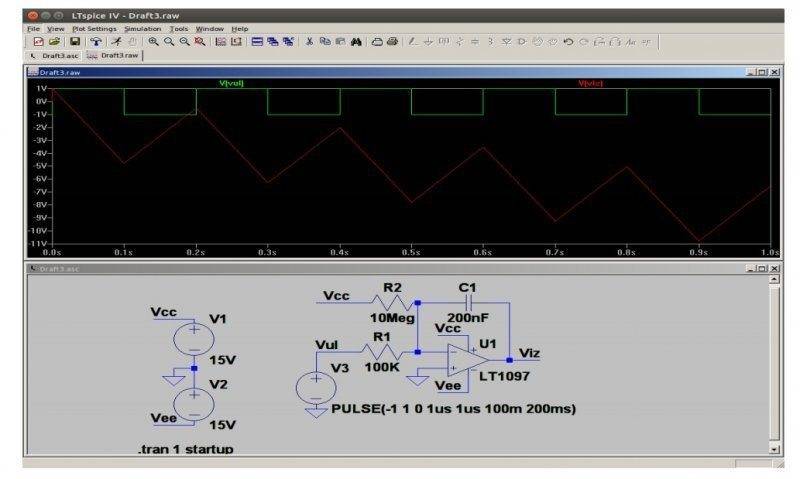
Then change capacitor's value from 200nF to 33nF and output voltage will be:
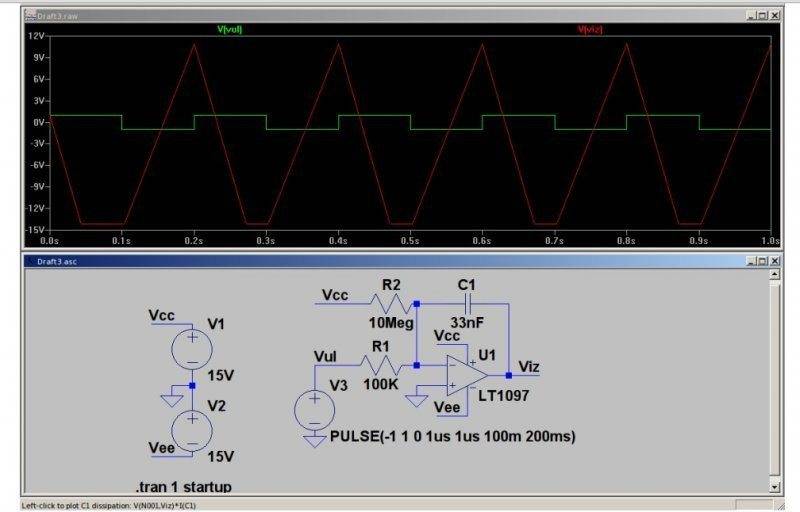
Explain why output voltages are different ( first has triangle shape and gradually decreases and second has cut off bottom and doesn't decrease).
Here is what I have done:
Since there are two sources, one DC and one time dependent pulse waveform, I used superposition method. When time dependent source is active, our circuit is:
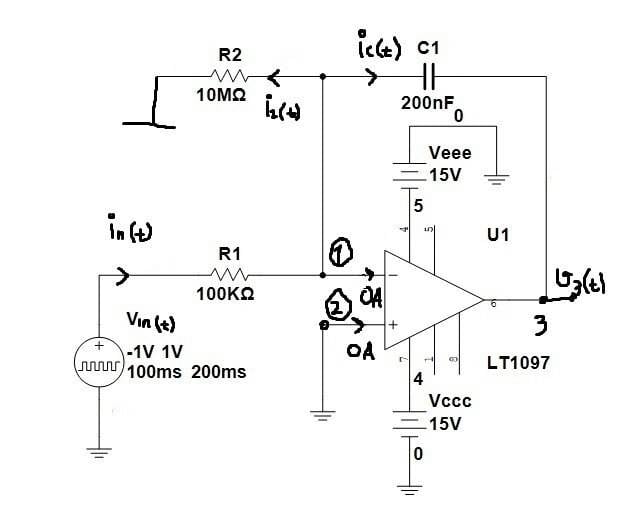
[tex]v2(t)=0\rightarrow v1(t)=0[/tex]
[tex]i2(t)=0\rightarrow iin(t)=ic(t)[/tex]
[tex]iin(t)=\frac{vin(t)}{R1}[/tex]
[tex]v3(t)+\frac{1}{C}\int ic(t)dt+R1iin(t)-vin(t)=0[/tex]
For positive input voltage [tex]vin(t)=1V[/tex] we have:
[tex]v3(t)=-\frac{1}{RC1}\int vin(t)dt=-50\int 1dt=-50t,\,\, 0\leq t\leq 100*10^{-3}s[/tex]
For negative input voltage [tex]vin(t)=-1V[/tex] we have:
[tex]v3(t)=-\frac{1}{RC1}\int vin(t)dt=-50\int (-1)dt=50t,\,\,100*10^{-3}s\leq t\leq 200*10^{-3}s[/tex]
But I don't know what to do next :(
Here is my task:
OPAMP circuit and output voltag are shown in image below. Assuming that OPAMP is ideal, come up with a solution by hand.
Then change capacitor's value from 200nF to 33nF and output voltage will be:
Explain why output voltages are different ( first has triangle shape and gradually decreases and second has cut off bottom and doesn't decrease).
Here is what I have done:
Since there are two sources, one DC and one time dependent pulse waveform, I used superposition method. When time dependent source is active, our circuit is:
[tex]v2(t)=0\rightarrow v1(t)=0[/tex]
[tex]i2(t)=0\rightarrow iin(t)=ic(t)[/tex]
[tex]iin(t)=\frac{vin(t)}{R1}[/tex]
[tex]v3(t)+\frac{1}{C}\int ic(t)dt+R1iin(t)-vin(t)=0[/tex]
For positive input voltage [tex]vin(t)=1V[/tex] we have:
[tex]v3(t)=-\frac{1}{RC1}\int vin(t)dt=-50\int 1dt=-50t,\,\, 0\leq t\leq 100*10^{-3}s[/tex]
For negative input voltage [tex]vin(t)=-1V[/tex] we have:
[tex]v3(t)=-\frac{1}{RC1}\int vin(t)dt=-50\int (-1)dt=50t,\,\,100*10^{-3}s\leq t\leq 200*10^{-3}s[/tex]
But I don't know what to do next :(