- #1
joneall
Gold Member
- 67
- 14
I'm reading "Bang!", by Brian May, Patrick Moore and Chris Lintott. On page 40, they say:
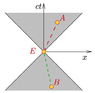
"So one [observer] may believe A preceded B by a minute, and another that A and B were simultaneous, it is impossible for any observer to see B preceding A. Hence cause and effect are preserved..."
But in the standard "paradox" of the pole and the barn (or the stretch limo and the VW-beetle garage), the runner sees the pole's forward end leave the garage before the back end enters, whereas the person standing next to the garage sees those two events in the opposite order.
Have I misunderstood something? Granted, I'm not sure what this has to do with cause and effect. Could that make the difference?
"So one [observer] may believe A preceded B by a minute, and another that A and B were simultaneous, it is impossible for any observer to see B preceding A. Hence cause and effect are preserved..."
But in the standard "paradox" of the pole and the barn (or the stretch limo and the VW-beetle garage), the runner sees the pole's forward end leave the garage before the back end enters, whereas the person standing next to the garage sees those two events in the opposite order.
Have I misunderstood something? Granted, I'm not sure what this has to do with cause and effect. Could that make the difference?