Parabolic track dynamics + calculus (Hard)

[Ruinmaniac]

Homework Statement

The problem is in the photo below:

https://www.physicsforums.com/attachment.php?attachmentid=71928&stc=1&d=1407288108

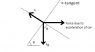
Text: Figure CP6.74 shows an accelerometer, a device for measuring the horizontal acceleration of cars and airplanes. A ball is free to roll on a parabolic track described by the equation y = x2, where both x and y are in meters. A scale along the bottom is used to measure the ball’s horizontal position x.

Homework Equations

F = ma
Possibly other kinematics equations.

The Attempt at a Solution

I can imagine how the problem would play out well in my head, and understand how the acceleration has an effect on the ball.
At any "x", slope is y' = 2x
I do not understand how to go from this slope to the angle (theta, see diagram) that represents the rotation of the tangent to the horizontal.

[EDIT] theta = tan^-1(2x) (just realized, man I am stupid sometimes lol)

The main forces that I think are acting on the ball are Fg, n, and force due to acceleration of vehicle in any direction, which i think points horizontally, the pic below shows my understanding of the problem:

https://www.physicsforums.com/attachment.php?attachmentid=71929&stc=1&d=1407288854

 

[Simon Bridge]

[EDIT] theta = tan-1(2x) (just realized, man I am stupid sometimes lol)

... this relationship is why the trig function is called "tangent" ;)
Good on you for leaving the mistake in though - that helps others.

Note: The acceleration of the car (what car?) does not produce a force.
The ball is "free to roll" - so it will roll back and forth along the track.
The forces on the ball are what produces the acceleration.
You have done problems with ramps before.

Note: $$\sin\left(\arctan x\right)=\frac{x}{\sqrt{1+x^2}}$$
http://en.wikipedia.org/wiki/List_o...mpositions_of_trig_and_inverse_trig_functions

 

[Ruinmaniac]

Sorry, that's my imagination talking, I imagined the ball and track inside a car and the car is moving to the left in this case. You are right there is no horizontal force acting on the ball but, when the "car" reaches constant acceleration, the ball should be stuck at one point, where the Fnet = 0. So there must be some force keeping the ball in that location right? So i just made a vector to help me out. I no longer have any idea on how to approach this. Sigh.

 

[Simon Bridge]

Oh I see what it is now.
OK - the situation is for a non-inertial frame so there will be a pseudoforce from the cars acceleration.
The vector sum of the forces should end up as zero for a constant acceleration.

 

[Ruinmaniac]

Yeah I did that however the unfortunate thing is that this has no answer key so I cannot even check. Regardless, you were extremely helpful, thank you!

 

[Simon Bridge]

No worries - real life does not have an answer key either... well, apart from actually doing it for real.
You need to get used to what the right answer "feels" like rather than relying on someone telling you.

You will probably be fine neglecting the moment of inertia of the ball - treat it as a block sliding on a frictionless track.
Gravity is F_g=-mgj and the normal force N has to cancel the net force perpendicular to the slope as usual.

Take care: if the ball has a positive x coordinate, then the acceleration of the car is in the -x direction.
So when a<0, x>0, and F_a points in the +x direction too ... it's easy to mess up the signs.

You will need to take sines and cosines of the arctangent ... the link I gave you will give you the shortcuts for that.
I cannot help you further because you have yet to show me the maths ;)