Parallel flow pipe network help

[hydronicengr]

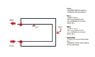
Let's say I have a simple parallel flow problem as shown in the attachment. The flow is pressurized and the downstream of the return goes back to a piping system that is negligible. It does not vent to atmosphere.

I've tried reading up on the subject, but I got stuck at a certain point. At point A, I know that the flow going in must equal the flow going out to the two pipes. Therefore, it will look like Q = Q1+Q2. Expanding Q1 and Q2 gives me V*A for each respective pipe.

I also know that the head loss of Pipe 1 must equal the head loss of Pipe 2. Expanding those equations, I find that I am faced with an unknown, which is the friction factor for each pipe. The friction factor can be explicitly calculated using the Swamee and Jain formula, but is dependent on the Reynolds Number, which is dependent on the flow velocity, which is ultimately dependent on the flow rate of each of the pipes. After getting the friction factor, everything else is easy. Simply plug the velocities from the head loss equations back into the Q formula shown above and solve for the unknown.

I know one can attain the correct friction factor value by many iterations, but is there a way without doing iterations by hand or by Excel and not fancy software?

Also, how would I find the total pressure loss of the system?

Thanks!

 

[W R-P]

I'd say assume no frictional losses, then solve in terms of bend losses etc. You can then obtain V1 in terms of V2,eg. V1= sqrt(k2/k1)V2 (Where k is the sum of the loss coefficients ,the Ks will vary for each pipe.). Then plug that into Q=A1V1 + A2V2 to get the value of V2, and subsequently Q2 and Q1. The pressure drop in each pipe is the same, so your pressure drop per unit weight (in metres) = k1(V1^2)/2g or k2(v2^2)/2g.
Hope this helps