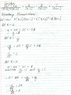- #1
Procrastinate
- 158
- 0
Partial Fraction Integration Check
Hello, I was just wondering whether my answer for my partial fraction integration question was right. Attached are three pages of my working but the answer is at the bottom of the third page (027) and the question is at the top of the first page (025).
Thanks.
Hello, I was just wondering whether my answer for my partial fraction integration question was right. Attached are three pages of my working but the answer is at the bottom of the third page (027) and the question is at the top of the first page (025).
Thanks.
Attachments
Last edited: