benca
- 19
- 0
- Homework Statement
- Use the graph to determine Planck's constant.
- Relevant Equations
- E = hf
Ek = hf - W
h = Planck's constant
f = frequency
W = work function
Attempt:
I was thinking of finding the slope of the graph but I only know the values for x = 10, y = 3 and y = 0. And without the y-intercept, I don't know the work function and can't solve for h. If you can't see from the picture, the last co-ordinate is (10,3) and the x-axis is measured in f x 10^14 Hz
I'm not sure what options I have left if I don't know how to figure out the slope or work function.
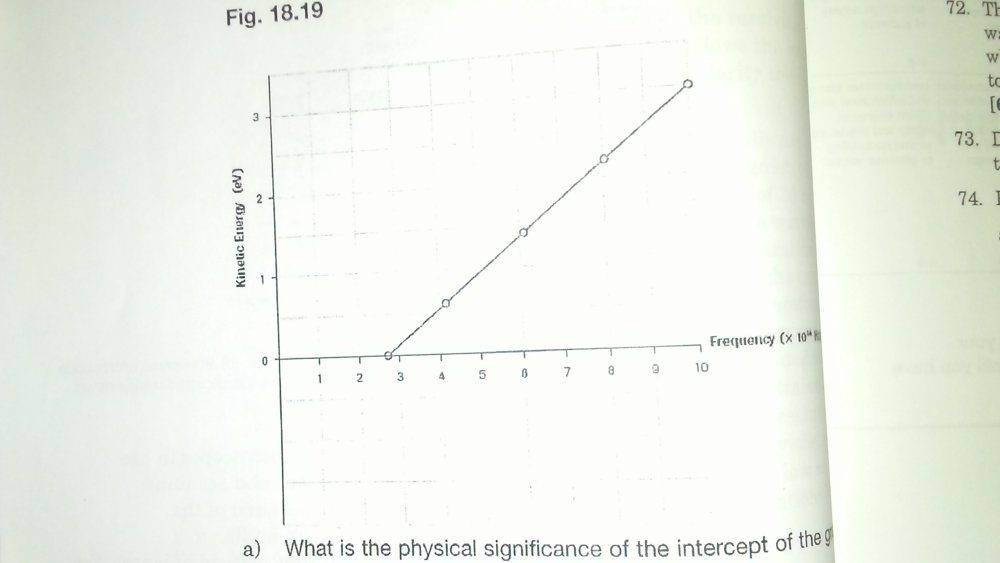
I was thinking of finding the slope of the graph but I only know the values for x = 10, y = 3 and y = 0. And without the y-intercept, I don't know the work function and can't solve for h. If you can't see from the picture, the last co-ordinate is (10,3) and the x-axis is measured in f x 10^14 Hz
I'm not sure what options I have left if I don't know how to figure out the slope or work function.