How Do You Calculate the Area of the Upper Crescent in Polar Coordinates?

[captainquarks]

I am asked to consider the following graph:

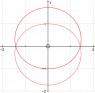
r²=a+sin(θ), where a=2

I have a picture of this plot, which I have attached,

We are asked to find the area of the upper 'cresent' of the curve, contained at the top

How would I go about calculating that?

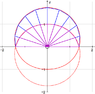
I've found that if I plot r=√(2+sinθ) and r=-√(2+sinθ) that this gives me the separate graphs individually, and that if I integrate from 0-π on the first one, then integrate from π-2π on the second one, if i subtract, i get the correct answer geometrically, using my graphing programme, but i don't know how to do this analytically? (i have attached another image to show the to sections - its the blue section i need)

Any help would be vastly appreciated, thank you

 

[captainquarks]

From my graphing programme, I've found the area should be 4.06-2.139 = 1.921 approximately, if this helps anyone?

 

[hivesaeed4]

I think your going to have to use cylindrical coordinates. From the graph it's evident that the limits of theta would be 0 to pi. The limits of r would be sqrt(2) to sqrt(3) (if your confused about how did I get these limits try finding the max and min values of r by playing around with the theta value).

 

[captainquarks]

I get where you have your limits by maximising sin in the range of 0-pi, giving r^2= 2 or 3... I've never done cylindrical coordinates before? We've never encountered them in lessons yet. Worrying

 

[captainquarks]

Never mind then lol. I know its definitely not cylindrical coordinates. Though.

 

[jssamp]

Is there any reason you are plotting r = -\sqrt{2+sinθ}? It would be easier if you use r = \sqrt{2-sinθ}. It plots the same circle but the intersecting points are coincident. The you could simply integrate

∫\frac{1}{2}((2+sinθ)-(2-sinθ))dθ

Since these two curves have the same period and starting point you can integrate from 0 to ∏