Polar Regions: Area, Arc Length, and Surface Area

[spacetime24]

Homework Statement

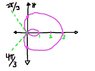
Consider the graph (see attachment) of r = 1 +2cos\Theta in polar coordinates. SET UP integrals to find
1. the area inside the large loop minus the area of the small loop.
2. the arc length of the small loop
3. the surface area of the surface formed by revolving the large loop about the initial ray.

Homework Equations

area A of the polar region
A = \int\frac{1}{2}(f(\Theta))^{2}d\Theta with upper limit b and lower limit a.

arc length AL of the polar region:
AL = \int\sqrt{r^{2}+(\frac{dr}{d\Theta})^{2}} d\Theta with upper limit b and lower limit a.

not sure what equation i need to figure out the surface area one

The Attempt at a Solution

I'm pretty much lost when it comes to the entire problem, and have no ideas where to start. Please help!

 

[ideasrule]

You've got the equations right. You just have to figure out what to use for the bounds. For 1, if you want to encompass only the larger arc, what should the upper bound be?

 

[spacetime24]

Well if the 4π/3 ray moved in a counterclockwise motion until the 2π/3 ray, then the ray would sweep the entire area of the large loop. But that would mean doing an integral from a lower bound of 4π/3 to the upper bound of 2π/3. This to me doesn't seem right since usually the lower bound is smaller than the upper bound.