- #1
UltimateSomni
- 62
- 0
For these four practice problems, I had little idea what the hell to do (plugging in seemed worthless), could anyone help? Sorry if this isn't what the board is suppose to be used for. Answers in spoiler tags.
If k and h are constants and x2+kx+7 is equivalent to (x+1)(x+h), what is the value of k?
Answer:
-----------------------------------------------------------------
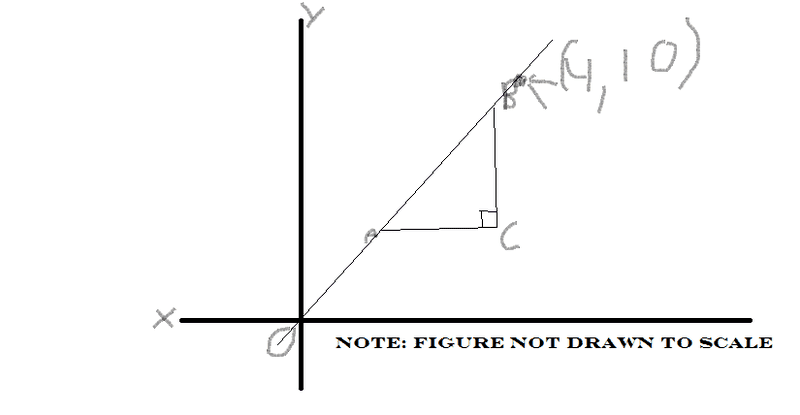
In the figure above, if the legs of the triangle ABC are parallel to the axes, which of the following could be the lengths of the sides of triangle ABC?
2,5,sqrt 29
2,5,7
3,3,3 sqrt2
3,4,5
4,5, sqrt41
Answer:
-------------------------------------------------------
Let the function f be defines as f(x)=2x-1. If 1/2f(sqrt t)=4, what is the value of t?
3/sqrt 2
7/2
9/2
49/4
81/4
Answer:
----------------------------------------------------------
If k is a positive integer, which of the following must represent an even integer twice the value of the odd integer?
2k
2k+3
2k+4
4k+1
4k+2
Answer:
It would be a great help if anyone could even point me into the right direction on these
If k and h are constants and x2+kx+7 is equivalent to (x+1)(x+h), what is the value of k?
Answer:
8
In the figure above, if the legs of the triangle ABC are parallel to the axes, which of the following could be the lengths of the sides of triangle ABC?
2,5,sqrt 29
2,5,7
3,3,3 sqrt2
3,4,5
4,5, sqrt41
Answer:
2,5 sqrt 29
Let the function f be defines as f(x)=2x-1. If 1/2f(sqrt t)=4, what is the value of t?
3/sqrt 2
7/2
9/2
49/4
81/4
Answer:
81/4
If k is a positive integer, which of the following must represent an even integer twice the value of the odd integer?
2k
2k+3
2k+4
4k+1
4k+2
Answer:
4k+2
It would be a great help if anyone could even point me into the right direction on these