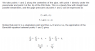You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Pressure at Points: What Does the Bernoulli Equation Tell Us?
AI Thread Summary
The discussion centers on the application of the Bernoulli equation to understand pressure differences at two points in a fluid system. Participants clarify that when fluid is in motion, pressure cannot be simply equated to static pressure, emphasizing the importance of velocity in the equation. There is confusion regarding the correct formulation of the Bernoulli equation, with participants urging for a proper understanding of its terms and their physical meanings. The significance of height differences in the equation is also highlighted, with a suggestion to use a specific datum for elevation reference. Overall, the conversation stresses the need for accurate application and comprehension of Bernoulli's principle to analyze fluid dynamics effectively.
Physics news on Phys.org
BvU
Science Advisor
Homework Helper
- 16,208
- 4,925
The velocity of the liquid makes a difference! Bernoulli.
werson tan
- 183
- 1
can you explain further?BvU said:The velocity of the liquid makes a difference! Bernoulli.
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,815
- 1,673
BvU means you must apply the Bernoulli equation to the two points to find out what the pressures are at those locations.werson tan said:can you explain further?
When the fluid is in motion, the pressure at any point is no longer equal to just the static pressure.
werson tan
- 183
- 1
can you explain how to apply the Beroulli's pronciple so that the P1 = pg(h1 +h2) ? but not P1 = pg(h1 +h2+h3) ?SteamKing said:BvU means you must apply the Bernoulli equation to the two points to find out what the pressures are at those locations.
When the fluid is in motion, the pressure at any point is no longer equal to just the static pressure.
BvU
Science Advisor
Homework Helper
- 16,208
- 4,925
Have you learned about Bernoulli already ? This is a very straightforward application!
werson tan
- 183
- 1
maybe there are some points that i have left out , can you point out please?BvU said:Have you learned about Bernoulli already ? This is a very straightforward application!
- 23,703
- 5,917
Please write out the Bernoulli equation for us (if you know it)?werson tan said:maybe there are some points that i have left out , can you point out please?
werson tan
- 183
- 1
P +z + (v^2) /.2g , wher v = velocity
- 23,703
- 5,917
Please try again. This is not an equation. I know this, because I don't see an equal sign. I also don't see any density in the equation. None of the terms in the equation are dimensionally consistent with one another. Please look it up and get it right this time. Otherwise, you won't be able to solve your problem.werson tan said:P +z + (v^2) /.2g , wher v = velocity
werson tan
- 183
- 1
it should be P/ y + z + (v^2) /.2g , where v = velocity , y = ρgChestermiller said:Please try again. This is not an equation. I know this, because I don't see an equal sign. I also don't see any density in the equation. None of the terms in the equation are dimensionally consistent with one another. Please look it up and get it right this time. Otherwise, you won't be able to solve your problem.
BvU
Science Advisor
Homework Helper
- 16,208
- 4,925
This is almost comical: 0084.png in post #1 says it all but apparently isn't acceptable for Werson. Do you find it difficult to understand the term with ##v^2## in the Bernoulli equation ?
(What Chet means is that this expression is a constant)
(What Chet means is that this expression is a constant)
- 23,703
- 5,917
This would be correct if that expression were set equal to a constant, and if that 0.2 in the denominator were a 2. Do you agree?werson tan said:it should be P/ y + z + (v^2) /.2g , where v = velocity , y = ρg
werson tan
- 183
- 1
how to relate it to the P1 ? why not P1 = P2 , which is ρg(h1 +h2 +h3) ?Chestermiller said:This would be correct if that expression were set equal to a constant, and if that 0.2 in the denominator were a 2. Do you agree?
- 23,703
- 5,917
Let's try to apply the Bernoulli equation to P1 and P2 to see what it tells us about their relationship. But, before doing that, do you understand the Bernoulli equation? Also, precisely what does z represent in the Bernoulli equation?werson tan said:how to relate it to the P1 ? why not P1 = P2 , which is ρg(h1 +h2 +h3) ?
werson tan
- 183
- 1
z represent the difference in height between 2 pointsChestermiller said:Let's try to apply the Bernoulli equation to P1 and P2 to see what it tells us about their relationship. But, before doing that, do you understand the Bernoulli equation? Also, precisely what does z represent in the Bernoulli equation?
- 23,703
- 5,917
You should think of z more as the elevation above a specified datum z = 0. In this problem, a logical choice for the datum would be the center of the pipe. Now please articulate what the Bernoulli equation means to you, or what each of the terms in the equation means physically.werson tan said:z represent the difference in height between 2 points
Similar threads
- Replies
- 2
- Views
- 890
- Replies
- 5
- Views
- 3K
- Replies
- 3
- Views
- 3K
- Replies
- 7
- Views
- 2K
- Replies
- 33
- Views
- 4K
- Replies
- 12
- Views
- 2K
- Replies
- 11
- Views
- 2K
- Replies
- 13
- Views
- 1K
- Replies
- 1
- Views
- 3K
Hot Threads
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math