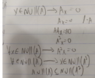Proving or Disproving Null Space Containment in F(n) for A and A^2

[sarumman]

Homework Statement

given

I am required to proove or disprove:[/B]

Homework Equations

rank
dim
null space

The Attempt at a Solution

I tried to base my answer based on the fact that null A and null A^2 is Contained in F (n)
and
dim N(A)+rank(A)=N
same goes for A^2.

 

[member 587159]

Why don't you just use the definition?

$x \in Null(A) \implies Ax = 0$

If the statement is true, you have to prove that $A^2 x = 0$. Can you show that?

 

[sarumman]

Why don't you just use the definition?

$x \in Null(A) \implies Ax = 0$

If the statement is true, you have to prove that $A^2 x = 0$. Can you show that?

thank you! you mean like so:

 

[member 587159]

Yes, the idea is certainly correct. The proof exposition can be better though. Here is how I would write it:

We want to prove that $Null(A) \subseteq Null(A^2)$, so let's take an arbitrary element $x \in Null(A)$. By definition, this means that $Ax = 0$. Since $A^2x = (AA)x = A(Ax) = A0 = 0$ (here we used associativity of matrix multiplication/function composition), it follows that $x \in Null(A^2)$, and we are done.

 

[PeterDonis]

@sarumman please use the PF LaTeX feature to post equations directly in the thread, instead of posting images. You can find help on how to use the LaTeX feature here:

https://www.physicsforums.com/help/latexhelp/