Bluestribute
- 192
- 0
Homework Statement
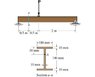
Determine the state of stress at point A on the cross section of the beam at section a−a. TakeP = 33kN .
Homework Equations
σ = My/I
The Attempt at a Solution
Moment = Fd = 33000N(500mm) = 165000000
Y = 90.71 (100-9.29, 9.29 being the Ybar of the little piece)
I = 22926666.67 (used on Part B and was correct)