CrazyNeutrino
- 99
- 0
Homework Statement
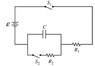
A circuit contains a capacitor of capacitance C, a power supply of emf E, two resistors of resistances R1 and R2 , and a switch S2 . Resistor R1 is in series with the power supply and R2 is in parallel with the capacitor and the power supply. S2 switches the branch that contains R2 (in parallel with the capacitor). Initially, the capacitor is CHARGED and S1 is closed while S2 is open. Switch S2 then gets closed at time t=0. Sketch the currents in resistance R1 and R2 as a function of time t.
Homework Equations
V=IR
Kirchoffs Loop and Junction Rule
Capacitor Differential equations
The Attempt at a Solution
I know that the solution is two exponential curves that asymptotically approach some current value from the top and from 0. I figured that the current in R1 is 0 when the switch is immediately closed while the initial current in R2 is E/R2 since the voltage across the capacitor and R2 must both equal E. My reasoning was that as t approaches infinity, the current in R1 and R2 will tend towards E/(R1+R2). However, I am not really sure why. I tried writing individual differential equations for the currents in R1, R2 and the capacitor but ended up confusing myself further. Could somebody please explain conceptually, what happens to the voltage across the capacitor and the currents in both resistors over time? I sort of understand what happens but don't particularly understand why.