Resolving forces in the direction perpendicular to a line

AI Thread Summary
To resolve forces perpendicular to a line, it's essential to sketch the appropriate triangle for the forces F1 and F2. Using the sine or cosine rule can help in determining the components of these forces. The key is to focus on the forces that act perpendicular to the lever with respect to the fulcrum A. By accurately labeling the forces and applying basic trigonometry, the correct answers can be derived. Understanding these concepts is crucial for solving similar problems effectively.
Bolter
Messages
262
Reaction score
31
Homework Statement
See below
Relevant Equations
N/A
Hi I'm very stuck on what to do for these 2 questions I got wrong

Screenshot 2020-10-16 at 12.17.44.png

Screenshot 2020-10-16 at 12.17.56.png


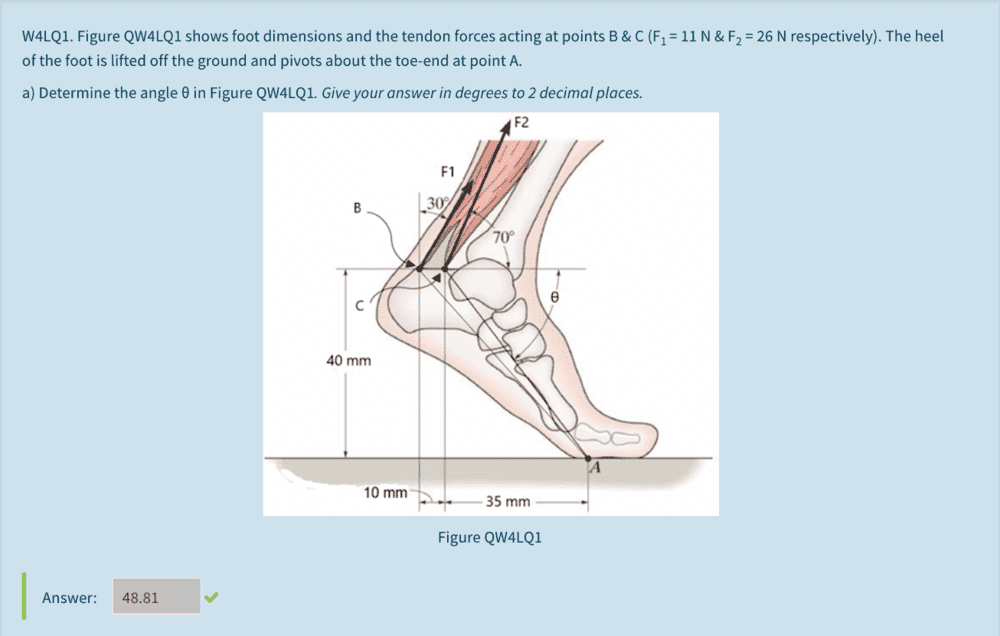
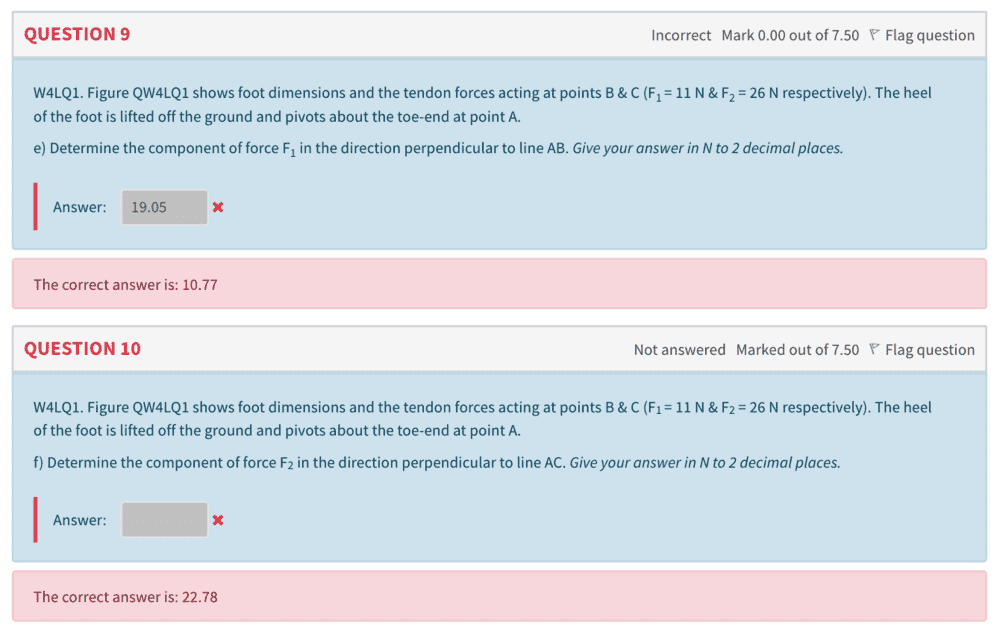
Can someone please help me on what triangle I need to sketch out in order to find the 2 components of forces for F1 and F2. I'm assuming you have to make use of the sine or cosine rule here

I'd be grateful for any help given! Thanks
 
Physics news on Phys.org
What have you done so far?
Remember that what counts here are the actual forces that are perpendicular to the levers, all respect to the fulcrum A.
 
  • Like
Likes Bolter
What are the horizontal and vertical components of force F1?
 
I actually managed to find the right answer at the end by drawing triangles and labelling the forces that are perpendicular to the line AB. Then with some basic trig I got the force needed
 
  • Like
Likes Lnewqban
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Vector-Force image and resolve force
Replies
27
Views
2K
Three equal forces applied to a rectangle, find net torque direction?
Replies
30
Views
4K
Solving Part (b): Find F3, F4, F1 and F2
Replies
7
Views
2K
To find the resultant of forces on a lamina
Replies
5
Views
3K
Force pulling on a string at an angle with a block at the other end
Replies
2
Views
1K
Plotting the graph of Friction Force vs. time (Laws of motion)
Replies
1
Views
2K
To find the angle between the ground and rods in limiting friction
Replies
5
Views
2K
Perpendicular forces acting in x and y directions
Replies
8
Views
2K
Electric Fields: calculate the resultant force
Replies
25
Views
2K
Hydrostatics Pressure - Finding thrust and resultants
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top