- #1
AI Thread Summary
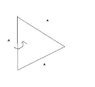
To find the rotational inertia of an equilateral triangle about the midpoint of its base, the discussion suggests calculating the moment of inertia about the center of mass first, then applying the Principal Axis Theorem by adding the product of the triangle's mass and two-thirds the length of the median. The user initially calculated 7/12 MA^2 but questioned its accuracy, noting that the known values for the tip and center are 5/12 MA^2 and 1/12 MA^2, respectively. There is a call for confirmation on the correct approach and results. The conversation emphasizes the importance of understanding the geometric properties and theorems related to the triangle's inertia.
- #2
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
Welcome to PF!
Hi joserse46! Welcome to PF!
Show us what you've tried, and where you're stuck, and then we'll know how to help!
Hi joserse46! Welcome to PF!
Show us what you've tried, and where you're stuck, and then we'll know how to help!
- #3
joserse46
- 4
- 0
Well what I am doing now is splitting the triangle up into two right triangles and finding the RI of on about it's tip (the tip that makes the right anlge), from there I could use the rod about the tip the intergrate from 0 to root 3 over 2A (the length og the triangle) But I sure there is an easier way to do this>
- #4
Bob S
- 4,662
- 8
First, calculate the moment of inertia about its center of mass, which is at the intersection of the three medians (drawn from each vertex to the center of the opposite side). Now add to this moment of inertia the product of the triangle's mass times 2/3 the length of the median from the vertex to the base. This latter term is called the Principal Axis Theorem.
- #5
joserse46
- 4
- 0
well i came to 7/12 MA^2 but that doesn't seem right since I know for a fact that it's 5/12MA^2 about it's tip and 1/12MA^2 about it's center. so shouldn't it be between that or I'm assuming too much
Hope someone can confirm this
Hope someone can confirm this
Neglect gravity other than that of water; neglect friction.
F1=ρgsh=1000*10*1*(1+4)=50000 N;
F1=ρgsh=1000*10*0.1*4=4000 N;
F3=50000-4000=46000 N?
Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system
$$M(t) = M_{C} + m(t)$$
$$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$
$$P_i = Mv + u \, dm$$
$$P_f = (M + dm)(v + dv)$$
$$\Delta P = M \, dv + (v - u) \, dm$$
$$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$
$$F = u \frac{dm}{dt} = \rho A u^2$$
from conservation of momentum , the cannon recoils with the same force which it applies.
$$\quad \frac{dm}{dt}...
TL;DR Summary: I came across this question from a Sri Lankan A-level textbook.
Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water.
I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
Similar threads
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math