gnarkil
- 26
- 0
Homework Statement
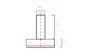
this is really getting confusing, i need to find the second moment of inertia Ixx and Iyy of the upside down beam, please see attachment
i've used and studied the other threads relating to the same topic and used wikipedia for the parallel axis theorem but am still confused, an explanation about the approach would be appreciated.
https://www.physicsforums.com/showthread.php?t=129591
http://en.wikipedia.org/wiki/Parallel_Axis_Theorem
http://en.wikipedia.org/wiki/Second_moment_of_area
https://www.physicsforums.com/showthread.php?t=88567
diagram dimensions:
a = 150/2 mm = 75mm
b = 150mm
c = d = 50mm
assume x-axis is horizontal and y-axis is vertical
assume origin is at the a distance a (150/2 = 75mm) from rhs and a distance c + b (150 + 50 = 200 mm) from top
Homework Equations
I used a textbook example, but the t beam was the opposite to the one i need
y_c neutral axis =
[ (b/2)(b2a) + (b + c/2)(2dc) ] / [ (b2a) + (c2d) ]
Ixx =
(1/12)(2a)(b^3) + (2ab)(y_c - b/2)^2 + (1/12)(2d)(c^3) + (c2d)(b + c/2 -y_c)^2
Iyy =
(1/12)(b)(2a)^3 + (1/12)(c)(2d)^3
The Attempt at a Solution
a = 150/2 mm = 75mm
b = 150mm
c = d = 50mm
using the above dimensions i got these values
y_c = 93.18 mm from bottom
Ixx = 841.5*10^5 mm^4
Iyy = 463.5*10^5 mm^4
i know they are wrong, but don't know why.
is the calculation for the second moment of inertia for a t beam with the same dimensions different to that of the identical beam that is upside down? why? would it be the same if i switched the base dimensions?**************************
update
i recaculated by y_c and got 50mm from bottom, and Ixx = 5.18125*10^-4 m^4
i still can't get Iyy
Attachments
Last edited: