- #1
Usiia
- 29
- 4
- Homework Statement
- Two Particles, each of mass m and having charges q and 2q respectively, are suspended from strings of length l from a common point. Find the angle θ that each string makes with the vertical.
- Relevant Equations
- Coulomb force definition with permittivity variable present.
I'd like someone to check that this solution is right, and if not, give me the point of failure and not the answer.
Thanks!
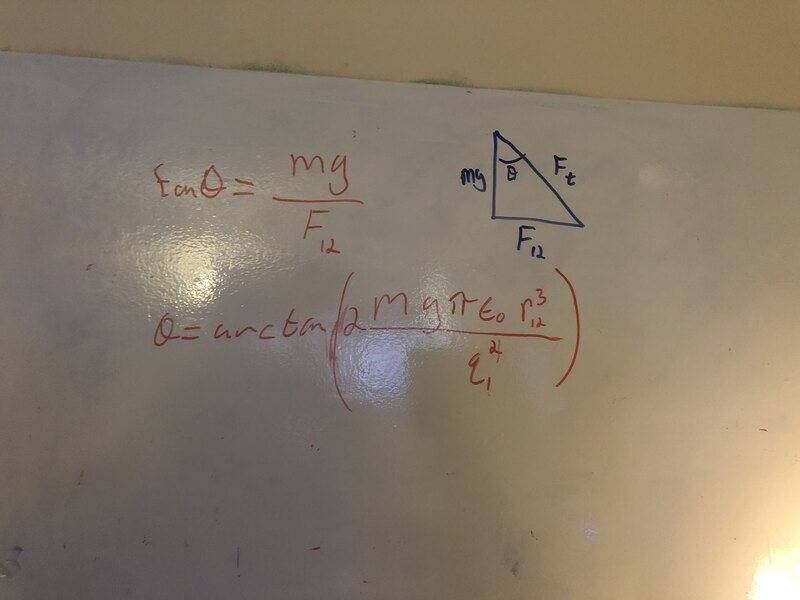
Thanks!