Slipping rolling cylinder friction

[xzibition8612]

Homework Statement

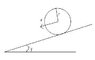
The cylinder is released from rest on the inclined plane. The coefficient of friction between cylinder and plane is μ. Determine the motion of the cylinder, assuming that μ is large enough to prevent slipping.

Homework Equations

The Attempt at a Solution

ok don't determine the motion. I have the solution in the textbook.

My question is about the friction. In my book it says "We are to assume the cylinder rolls. In this case the friction force f is an unknown and has a value satisfying 0≤f≤f_max where f_max=μN. After solving for f, we shall then impose the condition that it be less than μN, since we know the cylinder is not slipping"

Please note the friction vector is pointing to the right on the bottom of the cylinder.

I'm confused here about this friction. Why is f≤f_max? My intuition tells me if friction force is very big then the cylinder wouldn't roll. So if f≥f_max wouldn't the cylinder just not move? Why would it slip if f≥f_max? Thanks for explaining

 

[Doc Al]

The amount of friction force you need to prevent slipping is f. As long as f turns out to be less than the max possible, which is μN, then things are good. But if the f needed is more than the surfaces can deliver, meaning if f > μN, then you'll begin to slip. Not enough friction is available.

 

[xzibition8612]

so the maximum amount of friction available on this natural surface is uN. Meaning its not possible for f to be greater than this amount. So if it turns out f>uN, it means the cylinder will slip since not enough friction is present. Am I getting this correctly? Thanks.

 

[Doc Al]

so the maximum amount of friction available on this natural surface is uN. Meaning its not possible for f to be greater than this amount. So if it turns out f>uN, it means the cylinder will slip since not enough friction is present. Am I getting this correctly?

Yes. Exactly right.