Elbhi
- 5
- 0
I am having quite a time with this problem, I would appreciate any assistance.
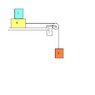
Block B, of mass mB, rests on block A, of mass mA, which in turn is on a horizontal table top . The coefficient of kinetic friction between block A and the table top is uK and the coefficient of static friction between block A and block B is uS. A light string attached to block A passes over a frictionless, massless pulley and block C is suspended from the other end of the string.
The Q is… What is the largest mass mC that block C can have so that blocks A and B still slide together when the system is released from rest?
My assumption is we want acceleration to be at the maximum that keeps block B over A. The larger the mC, I am assuming the larger the a. (I don’t know how to express that thought mathematically, if it is right)
This is what I did.
A: T-uK*(mA+mB)=mA*a
B: fs=uS*mB*g=mB*a…..fs=uS*g=a
C: mC-T=mC*a
FA-FB=T , I plug eq.A into FA, eq.B into FB, and solve for T in eq.3 to isolate the mC.
My answer for mC, which I know is wrong was...uk*(mA+mB)-us*mB
I am so confused. I have been struggling with this problem all day. I separated into components numerous times. (I don’t think that’s where my problem lays)
Someone plx help me to understand why I don’t understand.
Thanks
Block B, of mass mB, rests on block A, of mass mA, which in turn is on a horizontal table top . The coefficient of kinetic friction between block A and the table top is uK and the coefficient of static friction between block A and block B is uS. A light string attached to block A passes over a frictionless, massless pulley and block C is suspended from the other end of the string.
The Q is… What is the largest mass mC that block C can have so that blocks A and B still slide together when the system is released from rest?
My assumption is we want acceleration to be at the maximum that keeps block B over A. The larger the mC, I am assuming the larger the a. (I don’t know how to express that thought mathematically, if it is right)
This is what I did.
A: T-uK*(mA+mB)=mA*a
B: fs=uS*mB*g=mB*a…..fs=uS*g=a
C: mC-T=mC*a
FA-FB=T , I plug eq.A into FA, eq.B into FB, and solve for T in eq.3 to isolate the mC.
My answer for mC, which I know is wrong was...uk*(mA+mB)-us*mB
I am so confused. I have been struggling with this problem all day. I separated into components numerous times. (I don’t think that’s where my problem lays)
Someone plx help me to understand why I don’t understand.
Thanks