NeomiXD
- 31
- 0
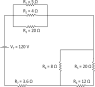
I've attached a conbined circuit diagram to this post. I have to solve the circuit. I know that I have to simplify the diagram into a series circuit to make it easier to solve, but I'm having trouble with a few parts in the diagram.
This is how I simplified so far:
1. I added R6 and R5 together using the series formula. I labeled it R8.
2. I added R4 and R8 together using the parallel formula. I labeled it R9.
3. I added R1, R2 and R3 together using the parallel formula. I labeled it R10.
This is where I'm having difficulty. Do I add R7 and R9 (from step 2) together using the series formula or do I leave it the way it is.
This is how I simplified so far:
1. I added R6 and R5 together using the series formula. I labeled it R8.
2. I added R4 and R8 together using the parallel formula. I labeled it R9.
3. I added R1, R2 and R3 together using the parallel formula. I labeled it R10.
This is where I'm having difficulty. Do I add R7 and R9 (from step 2) together using the series formula or do I leave it the way it is.