bendaddy
- 4
- 0
Homework Statement
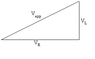
a) A pure resistance and a pure inductance are connected in series across a 100 V(rms) AC line. An AC voltmeter gives the same reading when connected across either the R or the L. What does it read? (Note: Meters read rms values.)
b) The magnitudes of R and L are altered so that a voltmeter across L reads 50 V. What will the voltmeter read across R?
Homework Equations
The Attempt at a Solution
Solution should be: a) 70.7V ; b) 86.7V