Solving Piecewise Integral: Help for Newbie Bailey

[MrBailey]

Hi from a newbie.

I have an apparently simple problem, but could use some guidance on how to do it.

I have the following function:

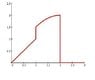
F(x)=\int^{x}_{0}f(t)dt,\ 0\leq x\leq3

where f(x)=\left\{\begin{array}{lll}1,&\mbox{ if }0\leq x<1\\2-x,&\mbox{ if }1\leq x<2\\0,&\mbox{ if }2\leq x\leq 3\end{array}\right

Is it as simple as:

F(x)=\left\{\begin{array}{lll}x,&\mbox{ if }0\leq x<1\\2x-\frac{x^2}{2},&\mbox{ if }1\leq x<2\\0,&\mbox{ if }2\leq x\leq 3\end{array}\right

A plot of F(x) for the interval would show discontinuities at x=1 and x=2.

Thanks for your help.

Bailey

 

[quantumdude]

Is it as simple as:

F(x)=\left\{\begin{array}{lll}x,&\mbox{ if }0\leq x<1\\2x-\frac{x^2}{2},&\mbox{ if }1\leq x<2\\0,&\mbox{ if }2\leq x\leq 3\end{array}\right

No, it's a little more complicated than that. For instace when you integrated over the second interval you treated it as follows:

\int_0^x(2-x)dx

However, F(x) is not defined as 2-x for 0\leq x<1, so it is not correct to start integrating that piece of the function at x=0. There is a similar problem with the third interval.

 

[MrBailey]

Okay...I can see I'm way off.

What would be the proper steps to take to find F(x) knowing the integral is from 0 to x?

Thanks for helping.

Bailey

 

[quantumdude]

The integral of your first piece is OK. You want to integrate it on the interval [0,x].

But your second and third pieces need to be integrated over [1,x] and [2,x], respectively.

 

[quantumdude]

Actually, the third piece is OK too, but only because it is zero.

 

[MrBailey]

So, integrating for each piece over the respective intervals would yield a plot like the one attached, for 0 <= x <= 3.

Is that correct, with the discontinuities at x = 1 and x = 2?

 

[MrBailey]

Good morning all.

Just want to find out if the graph above is correct.

Bailey