Like Tony Stark
- 182
- 6
- Homework Statement
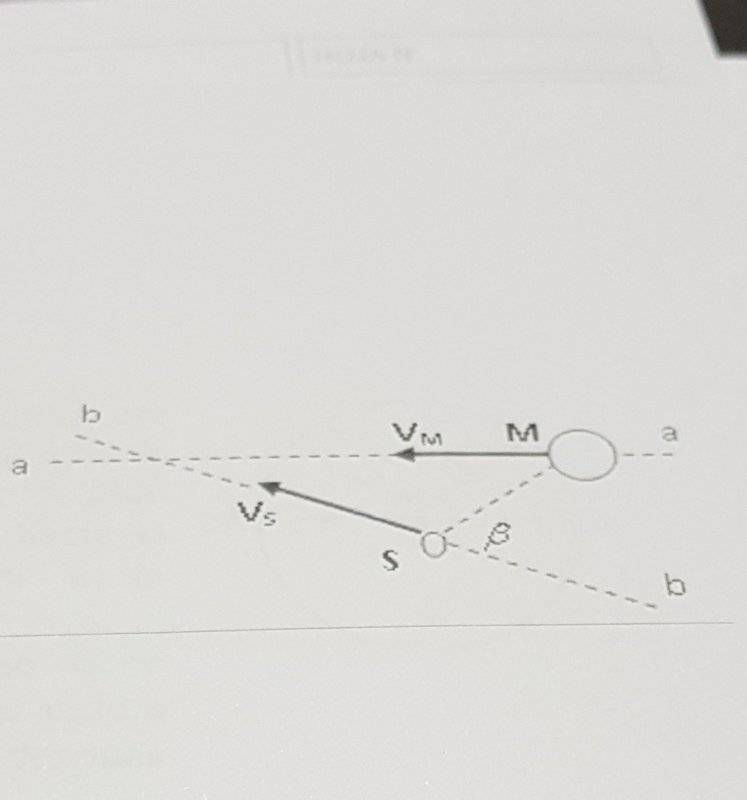
- The spaceship S approaches Mars following the trajectory ##b-b## with velocity ##\vec v_S=19.3 \frac{km}{s}## with respect to the Sun. If Mars has a velocity ##\vec v_M=24.1 \frac{km}{s}## along the trajectory ##a-a## with respect to the Sun, determine the angle between ##SM## and ##b-b## such that a person inside the spaceship "sees" that Mars is moving towards him.
- Relevant Equations
- ##\vec v_{B/A}=\vec v_B - \vec v_A##
As the problem asks for the spaceship's perspective, I know that I should take ##\vec v_S=0## and ##\vec v_M=24.1-19.3## because the motion is relative to the spaceship. Then, the relative velocity of Mars and ##SM## should have the same direction. If they have the same direction, that angle would be 90°, wouldn't it? I mean, probably I'm forgetting something, but that's the way I tried to do it