- #1
MyoPhilosopher
- 41
- 4
- Homework Statement
- Please see attached image
with distance between planets as 4x10^8m measured by you on the ship
- Relevant Equations
- t' = γ(t - ux/c^2)
with distance between planets as 4x10^8m measured by you on the ship
My attempt:
t' = γ(t - ux/c^2)
γ = 5/3
u = 0.8c
t = 0.9s
x = 4x10^8m
answer is: -0.278
Therefore not possible
My question is what if we traveled rightwards, from p2 to p1, would the answer change?
Should my above information make u = -0.8c instead of +?Thank you
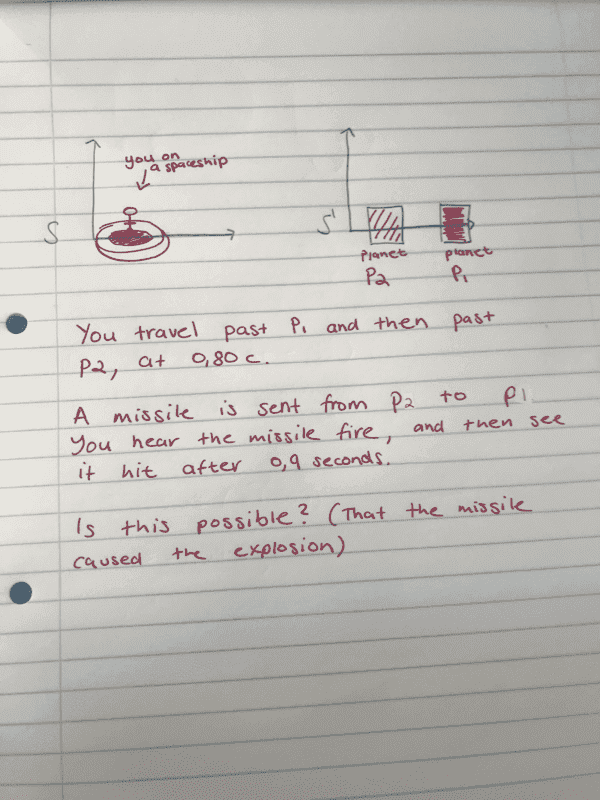
My attempt:
t' = γ(t - ux/c^2)
γ = 5/3
u = 0.8c
t = 0.9s
x = 4x10^8m
answer is: -0.278
Therefore not possible
My question is what if we traveled rightwards, from p2 to p1, would the answer change?
Should my above information make u = -0.8c instead of +?Thank you