Following your questions on other problems in the Olympiad paper, I looked through some more of it and discovered that your question in this thread also comes from there, as question 13. This sheds a different light on the sketched curve.
The illustration under Marker's Comments does seem to show hysteresis. It ought to have arrows on the curves to make it clearer, but it seems to show different paths for ascent and descent. The force would be weaker as the springs contract, so the upper part (shown as a straight line) is descent.
This interpretation is supported by the comments in d ii), but I am rather confused. First, you were asked to sketch the curve, and the given solution has no hysteresis, then d ii) reads as though you are given the graph with the hysteresis in the answer booklet.
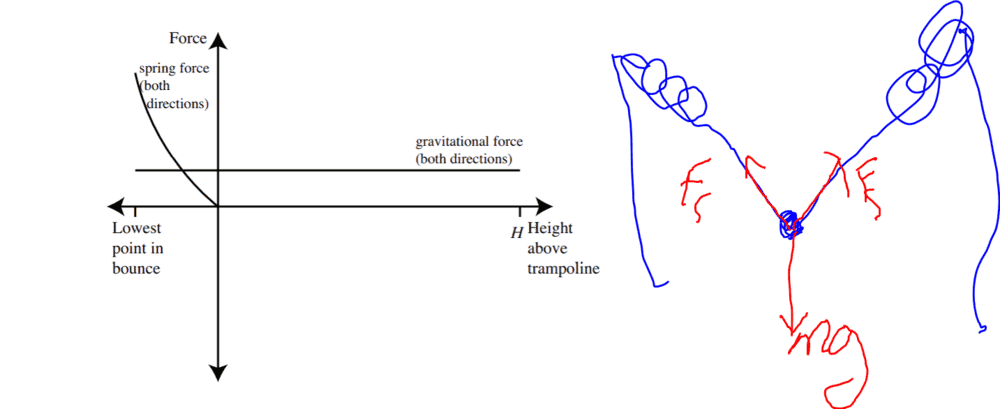
Anyway, this is not right. As I posted, we need to write the force as a function of h and constants. If the width of the trampoline is 2w then the extension of the springs is ##\sqrt{h^2+w^2}-1##, giving a vertical force component of ##kh(1-(1+\frac{h^2}{w^2})^{-\frac 12})## per spring.
For small h this approximates a total force of magnitude ##k\frac{h^3}{w^2}##. This is what explains the curve under "solution".
So the straight line portion in the diagram under Marker's Comments is spurious, whatever it was intended to illustrate. The correct picture would be two curves, each roughly cubic, but forming a hysteresis loop.
Edit:
Having looked at the answer booklet it is a little clearer - I was reading two consecutive questions as one.
Also, I see that the first graph was of force in the springs, which would be quadratic approaching the origin, whereas the second graph is force on the jumper, which is cubic as I wrote above.
The correct form of the second graph would be two cubics meeting at the origin. At the other end, they would be joined by a more-or-less straight vertical line.