Statics: Direction of Vertical/Horizontal Components

[Elfrid Payton]

1. The Problem

2. The Free Body Diagram

3. The Question

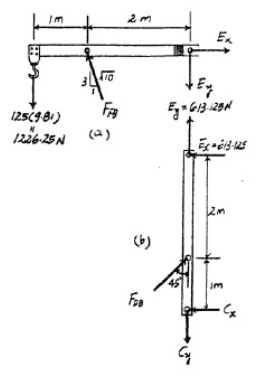
I've always had trouble determining the direction of the vertical and horizontal components in FBDs for statics problems, especially for a pin. Prior to looking at the solution, I wasn't sure on almost all of the directions of the vertical and horizontal components of forces. For member GE, I was sure that the mass of the engine would be pointing down, so I could just use equations of forces and moments to fix signs for the directions of the other forces. But for member EC, I wasn't sure on the directions of any of the forces, which meant that using equations of forces and moments would be of no purpose. Is there any way to analytically determine the direction of forces in statics problems?

 

[PhanthomJay]

When you are sure of a direction, denote it appropriately, always. Assume a direction of other forces in your step by step fbd's. Then once you know a direction, use it, and don't forget Newtons 3rd law when doing so.

In your first FBD, you know the weight force of the engine acts down...now you can assume the direction of the forces at E and F, but when summing moments about F, you quickly will discover that Ey must act down. So show it down. Then when summing forces in vert direction, you will quickly find that Fy must act up, and thus Fx must act left, and thus, Ex must act right. Then when looking at the next FBD , show force E directions in accord with Newton 3.

Your first step however is to determine what support reactions you can find, before taking frame apart.

 

[Elfrid Payton]

When you are sure of a direction, denote it appropriately, always. Assume a direction of other forces in your step by step fbd's. Then once you know a direction, use it, and don't forget Newtons 3rd law when doing so.

In your first FBD, you know the weight force of the engine acts down...now you can assume the direction of the forces at E and F, but when summing moments about F, you quickly will discover that Ey must act down. So show it down. Then when summing forces in vert direction, you will quickly find that Fy must act up, and thus Fx must act left, and thus, Ex must act right. Then when looking at the next FBD , show force E directions in accord with Newton 3.

Your first step however is to determine what support reactions you can find, before taking frame apart.

Ah, I can use reaction forces for the other member! Damn, that should have been really obvious.

So there's no real way to determine direction without using math?

 

[PhanthomJay]

Ah, I can use reaction forces for the other member! Damn, that should have been really obvious.

So there's no real way to determine direction without using math?

Well intuitively you can sometimes determine correct directions , like in your first FBD, the weight tends to rotate the member ccw about the piston, so the force at E vertically must act down to prevent that rotation . Not intuitive is the direction of the horiz comp of E. So do the math and don't forget Newton 3! And once you know the direction, be sure to note it correctly, or else the minus sign will drive you nuts.