You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Thevenin Equivalent: Understanding Polarity in Circuits
- Thread starter jegues
- Start date
AI Thread Summary
The discussion focuses on understanding the Thevenin equivalent circuit, particularly the calculation of Thevenin current (Ith) and resistance (Rth). Participants highlight common mistakes in circuit analysis, such as misidentifying parallel and series components and the importance of applying mesh analysis correctly. The conversation emphasizes the significance of understanding voltage polarities and current directions when analyzing circuits. Additionally, it clarifies that resistors do not have polarities; rather, it is the voltages and currents that define the circuit behavior. Overall, the thread serves as a resource for mastering Thevenin equivalents and mesh analysis in electrical circuits.
Physics news on Phys.org
xcvxcvvc
- 392
- 0
No. You calculated the wrong value for I-thevenin (and thus for R-th as well). I'm not following what you're doing to find it, so I can't pinpoint the mistake. I will say though, from my own experience, current sources trick people up often. I'd stick with the voltage source and just write a 2 loop mesh analysis with I2 being Ith.
By the way, in a simple circuit like this one with no dependent sources, you can short all sources and just find the equivalent resistance between the two points in question to find Rth.
By the way, in a simple circuit like this one with no dependent sources, you can short all sources and just find the equivalent resistance between the two points in question to find Rth.
xcvxcvvc
- 392
- 0
jegues said:Is this what you mean?
Yes, except you're not calculating the equivalent resistance correctly. That 15 ohm resistor only has 1 node in common with the 10 ohm resistor, so there is no way you can say they are parallel. Any parallel components share two nodes with each other whereas any series components share 1 node with each other.
jegues
- 1,085
- 3
xcvxcvvc said:Yes, except you're not calculating the equivalent resistance correctly.
What am I doing wrong?
Sorry if your help seems somewhat "hopeless" but I am indeed trying to understand this.
EDIT: Doh, 5//10 + 15 = 18.3,
Now the only part I have left to learn is the mesh analysis. If you don't have time to explain, I'll try googling and see what I can come up with.
Thanks again!
xcvxcvvc
- 392
- 0
jegues said:What am I doing wrong?
Sorry if you're help seems somewhat "hopeless" but I am indeed trying to understand this.
EDIT: Doh, 5//10 + 15 = 18.3
yes :) You may want to run through your Ith calculation again until you get the right value. You'll know now, because by using it, you'll calculate the same Vth as you just did.
jegues
- 1,085
- 3
xcvxcvvc said:yes :) You may want to run through your Ith calculation again until you get the right value. You'll know now, because by using it, you'll calculate the same Vth as you just did.
Well wait...
If I'm looking for my Ith and I know my Vth and Rth, can't I simply apply Ohm's Law?
Ith = Vth/Rth = 10/18.3 = 0.546A
?
xcvxcvvc
- 392
- 0
jegues said:Well wait...
If I'm looking for my Ith and I know my Vth and Rth, can't I simply apply Ohm's Law?
Ith = Vth/Rth = 10/18.3 = 0.546A
?
Yes. But doesn't it bother you that you incorrectly did the circuit analysis?
I'll explain some mesh analysis for you. wait.
First off, mesh analysis is useful for when you have voltage sources and resistors only. You can use it when there is a current source with a supermesh, but who cares about that for now. It uses Kirchoff's voltage law by saying "the voltage around a loop equals zero." Since you've already calculated Ith, I will use that circuit to teach you mesh (since i can't be doing homework for a poster if he already did it!).
We'll start by writing the KVL for each loop:
-V_s + V_{R_5} + V_{R_{10}} = 0
V_{R_{10}} + V_{R_{15}} = 0
We wrote these voltages with each loop having a defined current moving in a clockwise direction. As you should know, a resistor has + where the current goes in and a - where the current goes out. When writing the KVL for a mesh, just move along in a clockwise direction and write down the voltage with the sign of that which you approach. So you see the voltage source, we approached the negative sign, so I wrote -Vs. Also notice that the same 10 ohm resistor has current flowing into it in two different directions for what I wrote to be true. In the first loop, the current is entering from the top and in the second loop, current is entering from the bottom. We can do that! We just say some I entering the top = I1 - I2. Therefore, if we reverse the direction of the current, making it enter from the bottom, we'd write -i = I2 - I1.
So we then substitute for each voltage across the resistor using ohm's law (v = ir). The current in the first loop with the voltage source will be I_1 and the current in the second loop will be I_2:
-V_s + I_1 R_5 + V_{R_{10}} = 0
V_{R_10} + I_2R_{15} = 0
So the ones that I changed are the simple ones. the 5 ohm resistor has some current called I1 flowing through it clockwise and the 15 ohm resistor has some current flowing through it clockwise. But what about the center current? Like I said earlier, due to KCL, I going in from the top = I1 - I2. I going in from the bottom, the negative of the I going in from the top, = I2 - I1.
-15 + I_1 R_5 + R_{10}(I_1 - I_2) = 0
R_{10}(I_2 - I1) + I_2R_{15} = 0
So what happens if we chose the "wrong" direction of the current? What if the current is not truly moving clockwise? No problem! The current you calculate will just be negative. In fact, you could do mesh analysis with both currents going counterclockwise, both going clockwise, or 1 going clockwise and the other going counterclockwise. It just makes sense to do a uniform approach to keep consistency.
Also, for every new loop you add you add a new current. A general rule is n loops means n equations with n unknowns.
People always asked me how I wrote mesh loops so quickly, so I'll tell you since it seems to evade most people I know IRL. All you have to do is sum the total resistance in a loop and multiply it by the current of that loop minus the sum of any shared resistances multiplied by the current that is sharing the resistor plus any additional voltages (from voltage sources). Then you have your loop equation. The first one would be -15 + (5 + 10)i_1 - 10I_2 = 0 and the second would be -10i1 + (10 + 15)i2 = 0.
Last edited:
jegues
- 1,085
- 3
Thank you for all your help and the explanation of mesh analysis xcvxcvvc!
I've got a few questions.
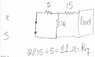
These seems to work flawlessly and is very easy to follow. However, the confusion that remains is the confusion within my intution. I've drawn a picture to show you where I've become confused.
I think you may have explained this in your post, but it's still not clear to me how the signs on the 10ohm resistors(I put it in red in the 2nd mesh analysis) are not interchanged.
Other than that everything makes sense!
Thanks in advance!
I've got a few questions.
All you have to do is sum the total resistance in a loop and multiply it by the current of that loop minus the sum of any shared resistances multiplied by the current that is sharing the resistor plus any additional voltages (from voltage sources).
These seems to work flawlessly and is very easy to follow. However, the confusion that remains is the confusion within my intution. I've drawn a picture to show you where I've become confused.
I think you may have explained this in your post, but it's still not clear to me how the signs on the 10ohm resistors(I put it in red in the 2nd mesh analysis) are not interchanged.
Other than that everything makes sense!
Thanks in advance!
Attachments
xcvxcvvc
- 392
- 0
jegues said:Thank you for all your help and the explanation of mesh analysis xcvxcvvc!
I've got a few questions.
These seems to work flawlessly and is very easy to follow. However, the confusion that remains is the confusion within my intution. I've drawn a picture to show you where I've become confused.
I think you may have explained this in your post, but it's still not clear to me how the signs on the 10ohm resistors(I put it in red in the 2nd mesh analysis) are not interchanged.
Other than that everything makes sense!
Thanks in advance!
On the top of the resistor, we can do a KCL, which states that the sum of the current entering and leaving the node equals zero, i.e. we did not create or destroy current/charge. So we will say the current in that branch is going from top to bottom.
We have I1 entering it (going clockwise) and I2 leaving it (going clockwise), and since we defined the current as going from up to down, we have some unknown current I_down leaving it. So we can KCL these:
I_down + I2 = I1
again, this is current leaving = current coming in.
Solving for this I_down, we get I_down = I1 - I2.
So what is the current going up then? We just need to multiply I_down by (-1) to get I_up. I_up = -I_down = -(I1 - I2) = I2 - I1
So when you write the second loop, you redefine the direction of the current as going up the branch, and you are still, therefore, entering the + node of the resistor.
If you really wanted to, you could keep I_down and then write -Idown * R_shared for the second loop. But... this would be -I_down = I_up = -(I1 - I2) = I2 - I1 . It's the same thing!
jegues
- 1,085
- 3
we defined the current as going from up to down
When did we do this? Was this implicit when I labeled the polarities of my 10 ohm resistor?
This is where I always get confused between polarities and direction of current.
berkeman
Admin
- 69,109
- 24,025
jegues said:When did we do this? Was this implicit when I labeled the polarities of my 10 ohm resistor?
This is where I always get confused between polarities and direction of current.
Resistors don't have polarities. Voltages have polarities and currents have directions. Your figure and equations look okay to me. With mesh analysis, you just pick the loop current directions (usually clockwise as you have used), and write out the KVL equations.
jegues
- 1,085
- 3
berkeman said:Resistors don't have polarities. Voltages have polarities and currents have directions. Your figure and equations look okay to me. With mesh analysis, you just pick the loop current directions (usually clockwise as you have used), and write out the KVL equations.
Doh! :)
What cases do you have negative voltages/currents? I seem to always make simple sign errors.
Should I be looking at the polarities of the voltage across the resistor and which terminal the current in entering?
For example, if current is leaving a node and passing through a resistor and experiences a voltage drop (+ to -) then that voltage will be positive, if it experiences a voltage rise (- to +) that voltage will be negative. Current leaving a node is positive and current entering a node is negative.
Is this really how we define positive and negatives in circuits or does it come down to how to define circuit aspects how your circuit?
Last edited:
Similar threads
- Replies
- 1
- Views
- 1K
Engineering
Find the Thevenin equivalent circuit
- Replies
- 42
- Views
- 6K
- Replies
- 17
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 12
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 9
- Views
- 5K
- Replies
- 2
- Views
- 1K
Engineering
Thevenin equivalent of resistor only circuit
- Replies
- 5
- Views
- 3K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Max water pressure allowable on solar panels
- Started by ethanesh
- Replies: 16
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math