1. Limited time only! Sign up for a free 30min personal tutor trial with Chegg Tutors
    Dismiss Notice
Dismiss Notice
Join Physics Forums Today!
The friendliest, high quality science and math community on the planet! Everyone who loves science is here!

Homework Help: Thevenin Resistance complex circuit with dependent sources

  1. Sep 15, 2012 #1

    Jd303

    User Avatar

    I am attempting to find Rth in the circuit attached however, I am totally lost. My work gets so messy and i seem to run around in circles. Can someone please explain to me how they would do this problem. Any help would be greatly appreciated
     

    Attached Files:

    Jd303, Sep 15, 2012
  2. jcsd
    Phys.org - latest science and technology news stories on Phys.org
  3. Sep 16, 2012 #2

    Simon Bridge

    User Avatar
    Science Advisor
    Homework Helper

    I'd do it the way the text books say ... open circuit current sources and close circuit voltage sources ... redraw the resulting circuit. If I'm reading that right, one of the resistors in in parallel with a short - so you can remove it.
     
    Simon Bridge, Sep 16, 2012
  4. Sep 16, 2012 #3

    scootypuffsnr

    User Avatar

    i think for thevenin's with a dependent source, you first have to find vth and then you s/c where vth is and then find the current through I-s/c
    after that then you get Rth = Vth/I-s/c
     
    scootypuffsnr, Sep 16, 2012
  5. Sep 16, 2012 #4

    uart

    User Avatar
    Science Advisor

    Hi jd303, have you learnt nodal and mesh analysis yet?

    With this circuit you've basically got two options.

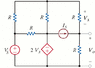
    1. Leaving all the sources intact, firstly solve to find the open circuit voltage at "Vo", and then solve once more with the output terminals shorted to find the short circuit current. The open circuit voltage is your V_thv and the ratio of V_oc/I_sc is your Z_thv.

    OR

    2. Set the independent sources to zero and apply an external 1 amp independent current source between the output terminals (directed toward the Vo +ive). Analyze using nodal analysis to determine the output voltage. The Thevenin resistance is numerically equal to this voltage.

    Method 2, in my opinion, is the easiest way to solve this if you're trying to find R_thv alone. I got it down to just 2 nodes (apart from the ref node) and three equations.
     
    uart, Sep 16, 2012
  6. Sep 16, 2012 #5

    Jd303

    User Avatar

    Hey uart,
    First of all thank-you for the explanation. Secondly yes I have covered nodal and mesh analysis as well as superposition.

    When Vs = 6, R=4kohms, and Is=1mA the answer is 2.9kohms

    I am still yet to get this, it may be due to some small error.

    I have labelled my nodes as follows and have attemped to find the open circuit voltage:
    Node 1: left-hand side
    Node 2: Top
    Node 3: Middle
    Node 4: Right - hand side
    and ref node at the bottom.

    Straight away i have put V1 as 6V

    After nodal analysis I finish with this
    3(V2) - (V3) - (V4) = 6
    -3(V2) + 2(V3) + 2(V4) = 2
    -V2 + 2V4 = 4

    If at all possible could you please point out my error, or explain how you were left with only 2 nodes and a reference, it would be greatly appreciated! Thanks
     
    Jd303, Sep 16, 2012
  7. Sep 17, 2012 #6

    gneill

    User Avatar

    Staff: Mentor

    In nodal analysis, nodes that are directly connected by voltage sources are amalgamated into supernodes. The reference node is not immune to this procedure :wink:
     
    gneill, Sep 17, 2012
  8. Sep 17, 2012 #7

    Jd303

    User Avatar

    Really sorry guys, just can not get this one out. Can someone please show me their node equations or other method. I keep getting the wrong answer for some reason. Thanks for your patience
     
    Jd303, Sep 17, 2012
  9. Sep 17, 2012 #8

    gneill

    User Avatar

    Staff: Mentor

    Voltage sources between nodes form supernodes. Even controlled sources participate, and the reference node is not immune to this treatment.

    A supernode can be identified as follows, leaving the indicated independent nodes:

    attachment.php?attachmentid=50956&stc=1&d=1347940775.gif

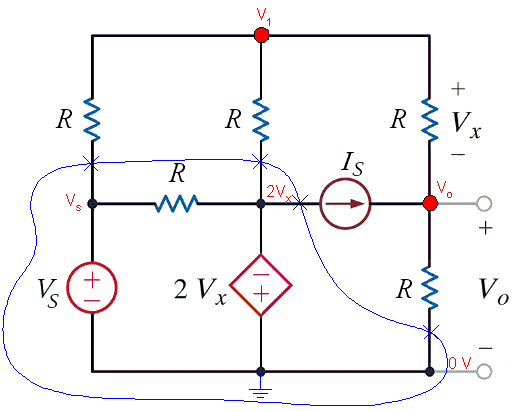
    You should be able to write the node equations, keeping in mind that Vx is equal to V1 - Vo.

    What do you get for the output voltage? How about the short-circuit current?

    You can start by showing us the node equations for the first case.
     

    Attached Files:

    gneill, Sep 17, 2012
  10. Sep 17, 2012 #9

    Jd303

    User Avatar

    Ok so i get:
    Node 1: (Vs-V1)/R - (V1-2Vx)/R - (V1-Vo)/R = 0
    Node 2: (V1-Vo)/R + Is - Vo/R

    Which leaves me with V1 - Vo = Vs
    and -V1 + 2Vo = Is*R

    Have I done anything wrong?
     
    Jd303, Sep 17, 2012
  11. Sep 18, 2012 #10

    gneill

    User Avatar

    Staff: Mentor

    The above looks okay. Note that I completed the second equation (red bit).
    I think you have a sign issue with the first expression of the pair. The second looks okay.

    Fix up the sign issue and solve for Vo.

    Then, short the output and using a similar approach find the short-circuit current, Io.
     
    gneill, Sep 18, 2012
  12. Sep 18, 2012 #11

    Jd303

    User Avatar

    Will Io not just equal Is if the output is shorted?
     
    Jd303, Sep 18, 2012
  13. Sep 18, 2012 #12

    uart

    User Avatar
    Science Advisor

    No, that would only be the case if we could assume the the current through the top resistor (the one marked with Vx) was zero. The current through that resistor is (V1-Vo)/R, which is not necessarily zero.
     
    uart, Sep 18, 2012
  14. Sep 18, 2012 #13

    uart

    User Avatar
    Science Advisor

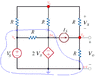
    This is the alternative method that I mentioned previously.

    The circuit simplifies down quite a lot. The resistor in parallel with the voltage source goes. Then you can do a Norton's source transformation on dependent source and combine some parallel resistors to end up with a circuit having only three resistors and two nodes.

    R_thv is numerically equal to Vo in the following circuit.
     

    Attached Files:

    uart, Sep 18, 2012
  15. Sep 18, 2012 #14

    Jd303

    User Avatar

    Ok so I have tried attempted the theory used from gneill.

    My final equations are:
    V1 + Vo = Vs
    -V1 + 2Vo = IsR

    Therefore:
    Vo = (Vs + IsR)/3
    V1 = (2Vs - IsR)/3

    And short circuit current equates to:
    Io = Is + (V1-Vo)/R

    Rth = Vo/Io

    Using this I still come up with the wrong answer, can anyone see where I have gone wrong??

    Once again thanks for the explanations, I feel like I am learning a lot even though i still cant get this one out
     
    Jd303, Sep 18, 2012
  16. Sep 19, 2012 #15

    gneill

    User Avatar

    Staff: Mentor

    The above looks good for the open-circuit case (finding Vo). You should point out at this point that the above expression for Vo is also Vth (the Thevenin voltage).
    ... and since Vo is shorted at this point ...
     
    gneill, Sep 19, 2012
  17. Sep 19, 2012 #16

    uart

    User Avatar
    Science Advisor

    I didn't get those equations. I think the problem is the node marked "2Vx" in reply #8 should have been labeled as "-2Vx".

    I went through this quickly just now and I got the same answer for R_Thv as I previously got using the "test source" method outlined in reply #12.
     
    uart, Sep 19, 2012
  18. Sep 19, 2012 #17

    gneill

    User Avatar

    Staff: Mentor

    Egads! You're right. Very careless of me, and good catch on your part.
     
    gneill, Sep 19, 2012
  19. Sep 19, 2012 #18

    uart

    User Avatar
    Science Advisor

    Yeah no problems. It's always the simple mistakes that catch me out too. :smile:
     
    uart, Sep 19, 2012
  20. Sep 19, 2012 #19

    Jd303

    User Avatar

    uart, using replacing the centre node with -2Vx I get the following equations:

    5(V1) -3(Vo) = Vs
    -V1 + 2Vo + IsR

    Io = Is + (V1 - Vo)/R

    Rth = Vo/Io

    Using the initial values set in comment #5 do you get Rth = 2.9kohms? I instead simply end up with the value of R
     
    Jd303, Sep 19, 2012
  21. Sep 19, 2012 #20

    Jd303

    User Avatar

    Or of coarse if anyone else can see my error, as i still can not get the correct answer to this problem it would be greatly appreciated. Thanks!
     
    Jd303, Sep 19, 2012
  22. Sep 19, 2012 #21

    gneill

    User Avatar

    Staff: Mentor

    Once you've fixed up the above, solve the first pair for Vo in terms of Is and Vs.

    When you change the circuit by shorting out the output (to find the short-circuit current), you're left with what is effectively a one independent node circuit. So you need to write a new node equation to find this new V1.
     
    gneill, Sep 19, 2012
  23. Sep 19, 2012 #22

    Jd303

    User Avatar

    Of coarse! Vo is not the same when the output is shorted, what an oversight! I didn't even pick that up from the hint that you tried to give me.

    Thanks, I dont think i could possibly get this wrong now (But you never know)
     
    Jd303, Sep 19, 2012
  24. Sep 20, 2012 #23

    uart

    User Avatar
    Science Advisor

    Yeah I think you've got it now. Once you fix those mistakes pointed out by gneill (the "not an equation" just needs to be set equal to zero) then you should definitely get the correct answer. (BTW. The answer turns out to be a fairly simple fraction of "R").
     
    uart, Sep 20, 2012
Share this great discussion with others via Reddit, Google+, Twitter, or Facebook