- #1
NickyuTse
- 9
- 0
#1, x , y are real number, x>=y>=1, 2*x^2-xy-5x+y+4=0,then x+y=?
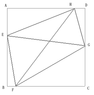
#2,look at the Attach image,ABCD is a square,and EFGH is a quadrangle,
angle BEG and angle CFH are both sharp angles. EG=3(units),FH=4(units),
the acreage of EFGH is 5, question: what is the acreage of ABCD?
#3 the quadratic equation about x is (k^2-6k+8)*x^2+(2k^x-6k-4)*x+k^2=4
and the two roots of x are integer,question: find out all the value of k
(k is a real number).
#2,look at the Attach image,ABCD is a square,and EFGH is a quadrangle,
angle BEG and angle CFH are both sharp angles. EG=3(units),FH=4(units),
the acreage of EFGH is 5, question: what is the acreage of ABCD?
#3 the quadratic equation about x is (k^2-6k+8)*x^2+(2k^x-6k-4)*x+k^2=4
and the two roots of x are integer,question: find out all the value of k
(k is a real number).