Heat Flow in Three Identical Rods of Metal

AI Thread Summary
In the discussion about heat flow in three identical rods forming an isosceles triangle, it is established that the temperature at point C is calculated as 3T/(1+√2). The rate of heat flow in rod BA is equal to that in rod BC, not CA, as initially suggested. The temperature gradient across rods BA and BC is confirmed to be the same. Some participants question the validity of the triangle's configuration and the temperature calculation at point C. Overall, both statements regarding heat flow and temperature gradients are affirmed as correct.
zorro
Messages
1,378
Reaction score
0

Homework Statement


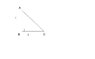
Three rods of identical cross-sectional area are made from the same metal, form the sides of an isosceles triangle ABC right angled at B. The points A and B are maintained at temperature T and √2 T respectively in steady state. Assume that only heat conduction takes place. Then

a) Rate of heat flow in BA is equal to rate of heat flow in CA

b) Temperature gradient across CA is equal to the temperature gradient across BA


The Attempt at a Solution



I got the temperature at C as 3T/1+√2.

Temperature at B > Temperature at A.
Rate of flow in BA will be equal to the rate of heat flow in BCA (not CA)
Again temperature gradient will be same across BCA

Both a and b are correct. I don't understand how. Help.
 
Physics news on Phys.org
Abdul Quadeer said:

Homework Statement


Three rods of identical cross-sectional area are made from the same metal, form the sides of an isosceles triangle ABC right angled at B.
How can isosceles triangle ABC be right angled at B?
 
Your calculation of temperature at C is wrong.
The two statements are true for BA and BC, rather BA and CA.
Check the problem.
 
How can isosceles triangle ABC be right angled at B?

Take a look at the figure.

Your calculation of temperature at C is wrong.

I found the temperature at C by equating the rate of heat flow through BC and CA.
I got the same answer after checking.
 

Attachments

  • Untitled.jpg
    Untitled.jpg
    3.4 KB · Views: 416

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

How Does Thermal Conductivity Affect Heat Transfer Between Two Water Vessels?
Replies
1
Views
1K
How Does Newton's Law of Cooling Affect Heat Loss Calculations?
Replies
2
Views
2K
Steady state heat flow: radiation and conduction
Replies
5
Views
3K
I How to measure average thermal conductivity of a metallic material?
Replies
1
Views
2K
Cooking (Thermodynamics) Problems
Replies
14
Views
4K
Heat Transfer: Finding temperature at the junction
Replies
3
Views
3K
Finding Increase in Temperature for Two Rods
Replies
3
Views
2K
Heat transfer through a cylindrical shell
Replies
3
Views
3K
Diffusion of energy by heat flow
Replies
1
Views
1K
Surface integral: Calculate the heat flow from a cylinder
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top