- #1
JohnnyGui
- 796
- 51
Hello,
I noticed something peculiar when looking at the Minkowski Diagram and I'm not sure how to interpret this.
Let observer A be the reference frame for the diagram and B someone who travels with respect to A.
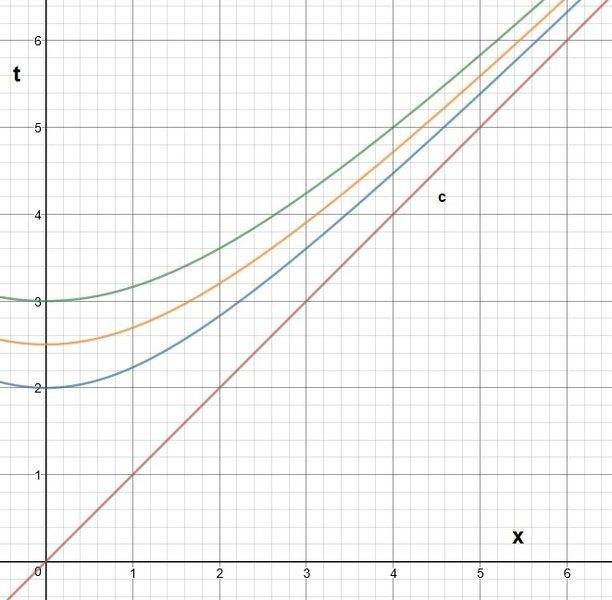
The red line is the displacement of light over time. The blue, yellow and green lines indicate fixed times of t = 2, 2.5 and 3 respectively according to someone who is traveling, such that if B intersects one of those lines at any ##x##, a time t=2, 2.5 or 3 has passed for B.
This means that, if B has a sufficient velocity to travel exactly on one of those lines, he won't experience any time (such a velocity is ofcourse not possible). You can see that those lines eventually have the same slope as ##c## so that light also doesn't experience time.
Now, let light leave A at t = 2 instead of t = 0. I'd then get the following diagram:
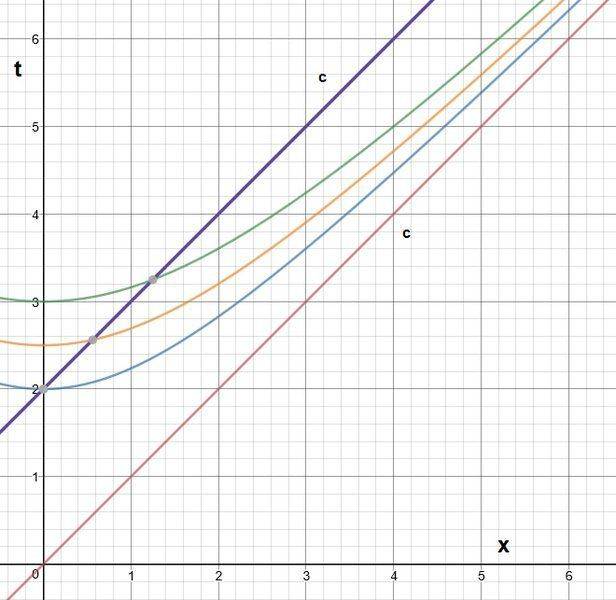
The purple line is light but now transposed and leaving A at t=0. You can see that this line intersects the blue, yellow and green lines. This implies that if B is leaving A at t=2 at the speed of light, he'd experience time lapse of 2.5 and 3 seconds over different distances of x when traveling, thus he wil experience time.
How is this possible while traveling at the speed of light shouldn't let someone experience time?
I have a feeling the blue, yellow and green lines are only with respect to ##c## if it starts from t=0 and starting from t=2 at the speed of light would need its own lines. Is this correct?
If so, then if a traveler C is leaving A at t=0 at ##c## (red line) and B is leaving A at t=2 also at ##c## (purple line), will C see B's clocking moving while B says that his own clock is not moving at all?
I noticed something peculiar when looking at the Minkowski Diagram and I'm not sure how to interpret this.
Let observer A be the reference frame for the diagram and B someone who travels with respect to A.
The red line is the displacement of light over time. The blue, yellow and green lines indicate fixed times of t = 2, 2.5 and 3 respectively according to someone who is traveling, such that if B intersects one of those lines at any ##x##, a time t=2, 2.5 or 3 has passed for B.
This means that, if B has a sufficient velocity to travel exactly on one of those lines, he won't experience any time (such a velocity is ofcourse not possible). You can see that those lines eventually have the same slope as ##c## so that light also doesn't experience time.
Now, let light leave A at t = 2 instead of t = 0. I'd then get the following diagram:
The purple line is light but now transposed and leaving A at t=0. You can see that this line intersects the blue, yellow and green lines. This implies that if B is leaving A at t=2 at the speed of light, he'd experience time lapse of 2.5 and 3 seconds over different distances of x when traveling, thus he wil experience time.
How is this possible while traveling at the speed of light shouldn't let someone experience time?
I have a feeling the blue, yellow and green lines are only with respect to ##c## if it starts from t=0 and starting from t=2 at the speed of light would need its own lines. Is this correct?
If so, then if a traveler C is leaving A at t=0 at ##c## (red line) and B is leaving A at t=2 also at ##c## (purple line), will C see B's clocking moving while B says that his own clock is not moving at all?