Total internal confinement of magnetic field

[tim9000]

Hi,
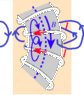
I heard it was possible if you symmetrically wind a toroid that you can get near total internal confinement of the magnetic field in the axial plane inside the toroid.
How is this possible? I imagine a section of a closed loop of wire on the face of the toroid core, yet I still imagine those imaginary B lines around the wire like a circle at some arbitary radius passing through core and air half-half. Which can't be the case.
Is there one of those pill-box or closed paths around a section explanations for how there is theoretically no B field in the air surrounding the toroid?

Cheers!

 

[mfb]

You can imagine the field of a single wire as having some field outside, but then you also have to add all the wires on the opposite side. They won't cancel perfectly, but they just leave a small net field, especially if you have some core material.

 

[tim9000]

Thanks for the reply mfb, what did you mean by

...especially if you have some core material.

sounds like you're saying that is detremental to the outside field cancelling.

Did you have rough picture on hand, or a link to a picture, I'm having trouble visualising what you said, when you said it 'cancels out with the wires on the oposite side', do you mean like if you drew a line from a wire on one side, through the centre to the other side of the toroid, that wire's B field would cancel out? Because that makes sense, INSIDE the toroid, as the oposite fields are facing each other, but what about the outside of the toroid where they're facing away from each other, or the top, where they're not facing each other? I'v attached a small picture example of these fields.

Thanks

 

[mfb]

Thanks for the reply mfb, what did you mean by sounds like you're saying that is detremental to the outside field cancelling.

The opposite - it will give even smaller fields outside.

Did you have rough picture on hand, or a link to a picture, I'm having trouble visualising what you said, when you said it 'cancels out with the wires on the oposite side', do you mean like if you drew a line from a wire on one side, through the centre to the other side of the toroid, that wire's B field would cancel out? Because that makes sense, INSIDE the toroid, as the oposite fields are facing each other, but what about the outside of the toroid where they're facing away from each other, or the top, where they're not facing each other? I'v attached a small picture example of these fields.

I don't have a picture, but that is the idea, yes. Inside, contributions from all cables add, outside, they cancel partially.

 

[tim9000]

The opposite - it will give even smaller fields outside.

I gathered so, I just don't understand your phrasiology.

I don't have a picture, but that is the idea, yes. Inside, contributions from all cables add, outside, they cancel partially.

You mean inside the core I assume, but I mean inside the central donut hole I can see them canceling (two blue circles of opposite direction interacting) but on the outside of the toroid you can see that the blue lines propagate in opposite directions, so how can they cancel?

Cheers

 

[mfb]

You mean inside the core I assume

Right.

so how can they cancel?

The cables "outside" (as seen from the central hole) give a field in one direction, the cables "inside" (as seen from the central hole) give a field in the opposite direction. Sure, they have different distances and geometry, a better analysis would need integrals over the whole structure.

 

[Baluncore]

Consider two single turns, on opposite sides of the toroid. The external fields will be in opposite directions because the current flow direction is opposite. Hence, there is total cancellation of the field at all points along the toroid axis. Elsewhere, at a distance, the difference in radius to the two loops will be small and so they will come close to cancellation.

There will be no field half way between two adjacent turns as the fields there are equal and opposite. There will be a slight field outside the windings but it will have very long field lines that form loops through the air, parallel with the outer surface of the toroid.

 

[tim9000]

Consider two single turns, on opposite sides of the toroid. The external fields will be in opposite directions because the current flow direction is opposite. Hence, there is total cancellation of the field at all points along the toroid axis

Is this picture what you were talking about:

?

According to Wiki: "Fig. 3. Toroidal inductor with circumferential current Figure 3 of this section shows the most common toroidal winding. It fails both requirements for total B field confinement. Looking out from the axis, sometimes the winding is on the inside of the core and sometimes it is on the outside of the core. It is not axially symmetric in the near region. However, at points a distance of several times the winding spacing, the toroid does look symmetric.[4] There is still the problem of the circumferential current. No matter how many times the winding encircles the core and no matter how thin the wire, this toroidal inductor will still include a one coil loop in the plane of the toroid..."
http://upload.wikimedia.org/wikiped...uctor-Simple_with_Circumferential_current.JPG
From:
http://en.wikipedia.org/wiki/Toroidal_inductors_and_transformers

But the picture (Fig 3.) looks just as symmetrical to me as Fig 1. on the wiki page so what's causing the lack of symmetry?
And what causes the circumferential current?

Sorry I just can't seem to get my head around this.

 

[Baluncore]

Is this picture what you were talking about:

No, your current shown in red should always travel in the same direction through the hole in the toroid.

And what causes the circumferential current?

In fig. 3. The circumferential current is because the helix of wire wound on the toroid has a component that follows the surface of the toroid.

 

[tim9000]

No, your current shown in red should always travel in the same direction through the hole in the toroid.

Ok so it needs to look like this:

When Wikipedia says:
"Figure 3 of this section shows the most common toroidal winding. It fails both requirements for total B field confinement. Looking out from the axis, sometimes the winding is on the inside of the core and sometimes it is on the outside of the core. It is not axially symmetric in the near region. However, at points a distance of several times the winding spacing, the toroid does look symmetric"

As far as I count there are an even number of windings, and if you cut the toroid in half it is a mirror of the other side. So do they mean that the exact distance of spacing between each winding isn't completely uniform or something, and THAT is where the lack of symmetry is coming in?

In fig. 3. The circumferential current is because the helix of wire wound on the toroid has a component that follows the surface of the toroid.

Oh, so do you mean by the nature of having to traverse point A to get to point B, that as I wind the toroid there is a slight component of the winding that is parallel to the plane of symmetry (toroid). But the closer the winding is to being prallel to the axis of symmetry the less circumferential current there will be? So it is unavoidable to atleast have a bit of circumferential current.

If you watned to maximise the circumferential current would you wind it so that each loop of wire was completed over 0-360 deg of the toroid? Because that way there would be almost no axis of symmetry (toroid) component.

Thanks heaps, look forward to your response.

P.S can you think of a way to measure or calculate the circumferential current?

 

[Baluncore]

Ok so it needs to look like this:

Yes, the wire always carries the current through the toroid hole in the same direction.

But the closer the winding is to being prallel to the axis of symmetry the less circumferential current there will be? So it is unavoidable to atleast have a bit of circumferential current.

No. For a simple helical coil there will always be one toroid of circumferential wire. By winding the coil back over itself, or threading the tail(s) back around the toroid to a common starting point, the circumferential current can be canceled exactly.
See fig 4, and fig 5, http://en.wikipedia.org/wiki/Toroid...for_total_internal_confinement_of_the_B_field

 

[tim9000]

Right, I was trying to figure that out before, so at the end of the winding the red wire becomes the white wire, cancelling out the toroidal plane component but adding to axial component, I see. Is that like Bifilar winding?
Also, Did you have an explanation regarding my question about where the lack of symmetry was coming in regarding:

When Wikipedia says:
"Figure 3 of this section shows the most common toroidal winding. It fails both requirements for total B field confinement. Looking out from the axis, sometimes the winding is on the inside of the core and sometimes it is on the outside of the core. It is not axially symmetric in the near region. However, at points a distance of several times the winding spacing, the toroid does look symmetric"

As far as I count there are an even number of windings, and if you cut the toroid in half it is a mirror of the other side. So do they mean that the exact distance of spacing between each winding isn't completely uniform or something, and THAT is where the lack of symmetry is coming in?

Is it just imperfection in spacing?

Thanks again

 

[Baluncore]

the red wire becomes the white wire,

Yes, the colour changes at the turn. They do make it difficult to see the joint.

Is that like Bifilar winding?

It is bifilar wound if you twist two wires together, then wind the twisted pair onto the toroid. You then have a four terminal 1:1 ratio transformer with very tight coupling.

Is it just imperfection in spacing?

No, it is because you are so close to the individual turns that they do not cancel exactly. At some distance cancellation gets better. The number of turns, odd or even, is unimportant, but the turns should be spaced evenly to get best confinement to the core.

 

[tim9000]

Ok, well if it isn't bifilar wound is there a name for the type of winding that cancells the circular current? (Like 'inversely wound' or something)

I'm really sorry to make you repeat yourself, I'm just really thick, but what was the lack of symmetry in the Figure compared to the Figure that was symmetrical, they still look the same to me.

Thanks and sorry!

 

[Baluncore]

It is called a "return winding". You are not thick, just human. Most toroid winders don't understand return windings.
Re: http://en.wikipedia.org/wiki/Toroidal_inductors_and_transformers
Figures 4, 5 and 6 all have a single gap in the winding along the toroid that is not passed by any wire.
The turns are still symmetrically spaced over the core.

It may be counter-intuitive, but that gap means the winding cannot have a circumferential current, hence it has better balance.

 

[tim9000]

Oh, Oh I think I see the gap you're talking about:

But what is it about the gap that "STOPS" the circulating current completely? I can imagine it would be a resistive path, but I wouldn't have thought it would 'stop' it completely...? Because the circulating current is in the core itself isn't it? Or is the wire doing more than I realize?

You could have the return wire running back along on the outside of the winding, rather than on the inside (as in Figure 4) ? Couldn't you? Just as long as it was carrying current in the opposite direction in the toroidal plane?

Maybe I was misunderstanding, the picture on the bottom left labled (Figure 1) "symmetric" is that actually symmetric? Maybe I just thought it was, because the picture on the bottom right (Figure 3) is: "Looking out from the axis, sometimes the winding is on the inside of the core and sometimes it is on the outside of the core. It is not axially symmetric in the near region." And as I said, I can't see a difference between the two, they both look symmetric to me.

Thanks again! This is really helping me

 

[Baluncore]

The term symmetry has too many interpretations to be useful. Fig.1, and Fig. 3, are topologically identical.

Yes, you have found the gap.
Current cannot flow across that gap, so there can be no net circumferential electric current.

It comes down to the area of a wire loop, when treated as an antenna.

Conceptually eliminate the toroidal core and consider the twisted wires that remain in place. Fig. 3, shows a major positive area enclosed. Figs. 4, 5 & 6 have low area because good cancellation of the minor positive and negative loop areas occur.

 

[Baluncore]

Because the circulating current is in the core itself isn't it?

The current flows in the wire. The magnetic flux flows in the core. The toroidal core usually has very poor conductivity, it is an insulator.

 

[tim9000]

Current cannot flow across that gap, so there can be no net circumferential electric current.

So cancellation of B on both ends of the gap is preventing any current from flowing around the circumference.

The current flows in the wire. The magnetic flux flows in the core. The toroidal core usually has very poor conductivity, it is an insulator.

But aren't we talking about the circular current as being from eddy currents inside the core? Dispite the high resistance of the core. Or are they not the problematic circular currents we've been talking about?

But what did the sentence: "Looking out from the axis, sometimes the winding is on the inside of the core and sometimes it is on the outside of the core." mean? Figures 1 &3 look the same to me as any other. If you put a treturn winding on Figure 1 or 3 would it be the same as Figure 5 or 6?

Thanks

 

[Baluncore]

But aren't we talking about the circular current as being from eddy currents inside the core? Dispite the high resistance of the core. Or are they not the problematic circular currents we've been talking about?

The currents we are talking about are in the wire. Think of the ferrite core as a ceramic insulator. There can be no eddy currents in an insulator.

But what did the sentence: "Looking out from the axis, sometimes the winding is on the inside of the core and sometimes it is on the outside of the core." mean?

A toroidal core has a hole, the wire runs down the inside wall of the hole, then up the outside of the toroid, over and down the inside again.On average the wound wire has a radius equal to the midline of the core.

Don't believe everything you read on wikipedia.

 

[tim9000]

The currents we are talking about are in the wire. Think of the ferrite core as a ceramic insulator. There can be no eddy currents in an insulator.

That's definitely been the point of confusion for me then, I was thinking that the wire path component on the plane was inducing circumferential eddy current in the core. But you're saying it's a net current in the wire on the toroidal plane that is the problem? (a problem because that causes magnetic nonsymmetry? is that the issue?)

Don't believe everything you read on wikipedia.

Ha. Isn't that the truth.

Many thanks again

 

[Baluncore]

But you're saying it's a net current in the wire on the toroidal plane that is the problem? (a problem because that causes magnetic nonsymmetry? is that the issue?)

Yes. Ideally, the magnetising current will not radiate from the wire as it does from a loop antenna.
That is a necessary condition for containment within a toroid of the magnetic field.

 

[tim9000]

I'm not really sure how it is not radiating from the wire, its just that one component is going into the core and the other aspect is being canceled by wire in the opposite direction.

Yes. Ideally, the magnetising current will not radiate from the wire as it does from a loop antenna.

If a setup in this way:

comprised of current flowing through infinitely long wires, around a toroidal core, existed, would it meet the criteria for total confinement?

Thanks heaps

 

[Baluncore]

would it meet the criteria for total confinement?

No, it would not be confined to the toroid. That is because there are many "toroids made of space" above and below your magnetic toroid. Each of those would have a circular magnetic field passing between the four inner and the four outer wires. The magnetic toroid could only gather a small amount of the field from nearby along the wire. The rest of the field would be through the air so it would not be confined.

Magnetic fields prefer paths through magnetic materials when such paths are available nearby. But when a much shorter loop through space is available, a field is not going to travel a long way through space and back just to pass through a magnetic particle.

You need to pull the wires tight against the toroid to eliminate the air-gap in order to achieve total confinement.

 

[tim9000]

No, it would not be confined to the toroid. That is because there are many "toroids made of space" above and below your magnetic toroid.

Interesting that, that would have an effect, I suppose I should have concidered them as a whole. So how about this modification (where the wire only exists along the face)

It must be hilarious for you to see how many ways I can get the concept so wrong. Hopefully you'll feel a bit rewarded when I finally do get it :P

Is there any mathematical link between increased inductance and total internal confinement? I'm very interested in this.

 

[Baluncore]

It must be hilarious for you to see how many ways I can get the concept so wrong.

No, it is just sad. Last time you expected currents of infinite extent to have fields totally confined to one small volume of space. This time you have electric current flowing in open circuits.

As current cannot flow around an open circuit, the current in your diagram must be zero and the resultant magnetic field must also be zero. If you confined the current into four small closed loops then the magnetic field would still not be totally confined because the current loops are too far apart. To cancel, the closed loop currents need to effectively cover the surface of the toroid.

The inductance, L, relates the energy, E, stored in the magnetic field to the current flowing in the electric circuit. E = ½ L i^2
http://en.wikipedia.org/wiki/Inductance

 

[tim9000]

No, it is just sad. Last time you expected currents of infinite extent to have fields totally confined to one small volume of space. This time you have electric current flowing in open circuits.

Whoa, steady on, it's just a hypothetical setup to illustrate the properties of the concept because I am interested primarily in the magnetic properies of the core itself, hence I am I am learning with blinkers on a bit. But I might add that hypothetical did infact remind me that to do that so I need to consider the wire too, so I'm not going to reconsider that asking it was a good idea. No need to patronise me, implying I don't even mearly understand electrical conduction and believe in magic wires.

As current cannot flow around an open circuit, the current in your diagram must be zero and the resultant magnetic field must also be zero.

Clearly you're not receiving the concept of my hyperthetical thought-experiment well and missing the point of my focus.

If you confined the current into four small closed loops then the magnetic field would still not be totally confined because the current loops are too far apart. To cancel, the closed loop currents need to effectively cover the surface of the toroid.

Again the illustration was an aid to understand my hyperthetical winding type and not a litteral skematic, I thought it unnecessary to draw many more at closer proximaty to replicate the toroid we have been discussing, however I was wrong, and I did mean there would be more than four loops around the toroid.

The inductance, L, relates the energy, E, stored in the magnetic field to the current flowing in the electric circuit. E = ½ L i^2

Of that much I am aware, specifically what I should have asked was: 'Does internal confinement effect the amount of stored energy present (inductance)?' As I'd have thought so.

 

[Baluncore]

Internal confinement reduces EM interference between components. Inductance rises as the area of the loops increase, so would you not expect total confinement to reduce the inductance to a minimum? Less confinement, more inductance?

 

[tim9000]

Flux is something I'm struggling with at the moment.

Internal confinement reduces EM interference between components.

So there'd be little to no flux linkage, reducing inductance.

Inductance rises as the area of the loops increase, so would you not expect total confinement to reduce the inductance to a minimum? Less confinement, more inductance?

I hadn't been thinking about loop area being really a factor as long as the loop is flush against the core. For instance, as long as the core is large the loop size can be large and the inductance can be high. So I'm not really following your line of reasoning, besides limiting EM interference, if it was so detramental to inductance I'm not sure why anyone would seek total internal confinement.
To answer your question, I'm trying to imagine two cores of the same size and same loop size, one with a return winding, one without, and I'm honestly not sure whether the energy stored in the core or energy in core + energy in the air is better for induction. I'd have thought just energy in core (internally confined) but that seems to be contrary to what you're implying with your question.

 

[Baluncore]

So I'm not really following your line of reasoning, besides limiting EM interference, if it was so detramental to inductance I'm not sure why anyone would seek total internal confinement.

Winding tight against the toroid reduces external coupling. It also reduces the length of wire needed to get the inductance required. A shorter wire length has less resistance, so the Q of the inductor is higher.

Adding a return winding very slightly reduces the inductance because the one circumferential current loop with an air core is cancelled, it slightly increases the resistance but greatly reduces the external coupling.

 

[tim9000]

Adding a return winding very slightly reduces the inductance because the one circumferential current loop with an air core is cancelled, it slightly increases the resistance but greatly reduces the external coupling.

Right, so if I have a return wire running back along the circumference of the toroid, it's only going to reduce the inductance by one turn (the turn that was coupling to air) and thus the inductance will be L = (N-1)*Flux / i
instead of L = N*Flux / i
?
Because when you said:

nductance rises as the area of the loops increase, so would you not expect total confinement to reduce the inductance to a minimum?

I thought you were implying there would hardly be any inductance of a totally confined toroid.

 

[Baluncore]

There are two ways to wind a coil onto a toroid. A turn can pass through the hole or it can run externally along the toroid without entering the hole. Those are two quite different magnetic situations.

A winding that passes through the hole has a closed path for the magnetic field that remains within the magnetic material of the toroid, with high inductance. An external winding has half it's magnetic field through air and so has much lower inductance per turn.

You cannot equate those two quite different perpendicular paths to combine them into the one inductance equation.
The number of turns on a toroidal core is a directional count of the number of times the same wire passes through the hole.

 

[tim9000]

A winding that passes through the hole has a closed path for the magnetic field that remains within the magnetic material of the toroid, with high inductance. An external winding has half it's magnetic field through air and so has much lower inductance per turn.

Agreed and understood, I'm just not sure why if it was totally confined then why would:

you not expect total confinement to reduce the inductance to a minimum? Less confinement, more inductance?

" as I said, I'd have thought better confinement in the core, more inductance.

Ok, say that N is the amount of loops the wire does around the core, through the hole, so a return path does nothing to that inductance equation?

 

[Baluncore]

Ok, say that N is the amount of loops the wire does around the core, through the hole, so a return path does nothing to that inductance equation?

The one turn circumferential loop that can be canceled by a return winding is perpendicular to the wanted toroidal current and field, so the total inductance is the simple sum of those two inductances in series. When you introduce a return winding, you cancel the smaller external inductance and so only the toroidal inductor remains.

That is why a return loop compensated toroidal winding will have a significantly lower external field, but at the cost of a slightly lower total inductance.

 

[tim9000]

Meaning total inductance = L from loops through hole of toroid + L from the one resulting which is perpendicular to the loops through the hole (which can be canceled and sacrificed for the sake of no EMI)?

If you wouldn't mind, do you think you could please comment on this:
https://www.physicsforums.com/threads/induction-and-flux-linkage-clarification.792734/