alesdiazdeo
- 3
- 0
- Homework Statement
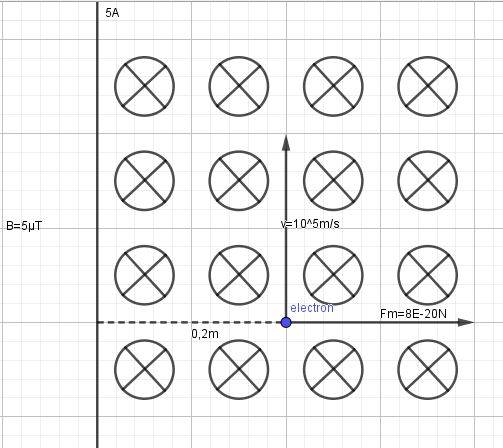
- There's an infinite vertical wire which produces 5Amps. An electron is 0.2 meters apart with a velocity of 10^5 m/s in the same direction of the wire. The wire is creating a magnetic field which alters the trajectory of the electron. I need to know to the function which represents it.
- Relevant Equations
- Fm(magnetic force)=q(v x B) (charge times vectorial multiplication of velocity and magnetic field)
Without vectors it's just Fm=qvB
B(magnetic field)=nu/2pi * I/R (I=current intensity, R=distance)
nu/2pi=2*10^-7 (it's a constant)
B equals 50*10^-7 T (at first instance)
Fm equals 8*10^-20 N (at first instance)
I know Fm is perpendicular to the velocity, and I know the estimation of the trajectory (somewhat similar to the curve y=lnx).
Since I think vertical velocity will be constant, only changing the x component, I tried summing the Fm and the B formula, creating a bigger formula which I think represents the growth on the Y axis of the final desired formula dependent to R. That's what I want, not a formula that depends on time but a formula that depends of the distance to the wire (R).
Fm equals 8*10^-20 N (at first instance)
I know Fm is perpendicular to the velocity, and I know the estimation of the trajectory (somewhat similar to the curve y=lnx).
Since I think vertical velocity will be constant, only changing the x component, I tried summing the Fm and the B formula, creating a bigger formula which I think represents the growth on the Y axis of the final desired formula dependent to R. That's what I want, not a formula that depends on time but a formula that depends of the distance to the wire (R).
Last edited: