amalone
- 2
- 0
Homework Statement
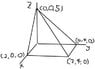
Write out the triple integral for the volume of the solid shown in all six possible orders. Evaluate at least 2 of these integrals.
Homework Equations
I attached a picture of the figure. The front : x/2+z/5=1
right : y/4+z/5=1
The Attempt at a Solution
I really need help with the possible orders and not the actual integration.
I figured out two different orders but I'm not sure how to post them properly