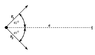
Two forces at 45 pull an object distance of 14. What is work by both forces?

  • Thread starter Thread starter evan b
  • Start date Start date
  • Tags Tags
    Forces Pull Work
AI Thread Summary
To calculate the work done by two forces of 7 N each pulling at a 45-degree angle over a distance of 14 m, the forces must be resolved into components. The correct approach involves determining the resultant force using the Pythagorean theorem, yielding a force magnitude of approximately 9.9 N. The work done is then calculated using the formula W = F * d, where F is the effective force in the direction of motion. The confusion arises from miscalculating the resultant force and not applying the correct distance in the work formula. Ultimately, the accurate work done by the two forces is approximately 138.6 J.
evan b
Messages
10
Reaction score
0
What is the work done by the two forces together in moving an object a distance of d = 14 m as shown in the diagram? The magnitude of each force is 7 N.
 

Attachments

  • prob39.gif
    prob39.gif
    2.9 KB · Views: 701
Physics news on Phys.org
evan b said:
What is the work done by the two forces together in moving an object a distance of d = 14 m as shown in the diagram? The magnitude of each force is 7 N.

Separate the forces into components. What you are interested in are the force components in the direction that the block is actually moved.

W = f * d.
 
ya, so i found force by sqrt of 7^2 + 7^2. then i multiplied it by 7 and go 69.30 J. What am i doing wrong?
 
evan b said:
ya, so i found force by sqrt of 7^2 + 7^2. then i multiplied it by 7 and go 69.30 J. What am i doing wrong?

Isn't the distance it's moved 14?
(The sqrt of 98 looks ok for the force in the direction of motion.)
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

(Magnetism) Magnetic pull force on a steel ball
Replies
4
Views
2K
How do I find the work done for a 100 N downward force?
Replies
4
Views
2K
Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations
Replies
15
Views
149
My Mistake? Understanding Friction Force & Work Done on Snowy & Icy Surfaces
Replies
29
Views
2K
Solving Confusions on Pulling a Spool
2
Replies
90
Views
5K
The Work of Friction: Explained in .32m
Replies
8
Views
2K
Coefficient of friction of a sandwiched body
Replies
15
Views
848
Work Pulley Problem with constant speed
Replies
2
Views
1K
External forces required to move an electric dipole quasi-statically
Replies
14
Views
1K
Rolling without slipping problem
Replies
42
Views
3K

Hot Threads

Recent Insights

Back
Top