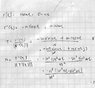Unit tangent vector vs principal normal vector

[BvU]

by the way, what is $v$

As I said, learn yourself to clearly designate vectors as vectors and scalars as scalars.

There are a few possibilities for the notation.

The one in your textbook is

• vectors are bold
• vector norms are written with double vertical lines ($\ \|\$)

and is not very suitable for handwriting. If your class doesn't have it's own standards, I would advise:

• vectors are written with an arrow above ($\ \vec r\$)
• a single | is enough for a norm ($\ |\vec r| \$ )

Once you are more experienced you can make it easier by dropping the | : $\vec r$ is the vector, $r$ is the norm. Not now, later.
Stay with your standard. Use it consistently.

You are going too fast without a drivers license. Re-post #57 with a decent notation.

In answer to your #56: what is $v$ :

It is common to designate a position vector as $\vec r$.

In Cartesian coordinates a 2D $\ \ \vec r = (x,y) \$ and a 3D $\ \ \vec r = (x,y,z)$.
x and y may depend on time and you get e.g. $\ \ \vec r(t) = (x(t),y(t)) \$
​

The time derivative is the velocity vector, commonly designated as $\vec v$. So $\vec v = \displaystyle d\vec r\over dt$.

In Cartesian coordinates a 2D $\ \ \vec v = (v_x,v_y) = \left (\displaystyle {dx(t) \over dt}, \displaystyle {dy(t) \over dt} \right) \$,
often abbreviated with a quote for ${d\over dt}$. E.g. a 3D $\ \ \vec v = (x',y',z')$.
​

The time derivative of the velocity vector is the acceleration vector, commonly designated as $\vec a$. So $\vec a = \displaystyle {d\vec v\over dt}$.

In Cartesian coordinates a 2D $\vec a = (a_x,a_y) = (x'', y'')$
​

I could retype all 385 pages of Paul's excellent pdf, but I suggest you read through it on your own -- just to get familiar. And make a lot of exercises to build up experience.

 

[BvU]

Now I start to double-post too.

 

[chetzread]

http://tutorial.math.lamar.edu/Classes/CalcIII/Curvature.aspx
well , can you explain how to get the circled part ? my problem is this.

 

[BvU]

I spent quite some time typing #61. #63 is identical to post #1 in the thread that was merged into this one. It looks as if you don't want to learn the language of simple vectors and vector calculus, so: yes I can but you wouldn't understand. Is there a good reason for that ?

 

[chetzread]

I spent quite some time typing #61. #63 is identical to post #1 in the thread that was merged into this one. It looks as if you don't want to learn the language of simple vectors and vector calculus, so: yes I can but you wouldn't understand. Is there a good reason for that ?

I spent quite some time typing #61. #63 is identical to post #1 in the thread that was merged into this one. It looks as if you don't want to learn the language of simple vectors and vector calculus, so: yes I can but you wouldn't understand. Is there a good reason for that ?

 

[chetzread]

Ok, here is after correction

 

[BvU]

So far
we have $\vec r\qquad$

don't forget the arrow over the $r$ -- or some other way to clearly mark it as a vector
don't forget the brackets
$\qquad \vec r(t) = (cos\omega t,\sin\omega t)\ \$ which was the given data.​

we have $\vec r'\qquad$ which is $\vec v$ (so $\vec v$ is NOT your ${r'\over|r'|}$ !)

don't forget the arrow over the $r'$ -- or some other way to clearly mark it as a vector
don't forget the brackets
$\qquad \vec r'(t) = (- \omega \sin\omega t,\omega\cos\omega t)\ \ = \omega (\sin\omega t,\cos\omega t)\ \$ .​

We see that $|\vec r| = 1$ (right ?) and we see that $|\vec r'| = |\omega|$ (right ?)

But then you go all wrong by thinking that $\vec T$ is not a vector.
And what you do to find $\vec N$ is a mystery to me. Again, you write it as a number, which it is NOT. $\vec N$ is a vector !

 

[BvU]

http://tutorial.math.lamar.edu/Classes/CalcIII/Curvature.aspx
well , can you explain how to get the circled part ? my problem is this.

Do you know how to calculate the norm of a vector product such as $\ \vec r'\times \vec r'' \$?

 

[chetzread]

But then you go all wrong by thinking that ⃗T\vec T is not a vector.
And what you do to find ⃗N\vec N is a mystery to me. Again, you write it as a number, which it is NOT. ⃗N\vec N is a vector !

sorry , for T , it should be (-w sin wt i + w coswt j ) / w
, similarly ,
for N , it should be = (-(w^2)((coswt)^2) i - (w^2)((sinwt)^2) j ) / (w^2)
Again , here's the formula have in my book

 

[chetzread]

Do you know how to calculate the norm of a vector product such as $\ \vec r'\times \vec r'' \$?

do you mean express it in form of unit vector ?

 

[BvU]

do you mean express it in form of unit vector ?

why not answer a question with an answer instead of with a question ?

To your question: No. Unit vectors are boring : they have norm 1.
In this case you are (of course ) not interested in the vector itself (*), but in the length of that vector product. That is $\kappa$, a number.

(*) but you can ask yourself which way it is pointing, e.g. for a particle in a circular trajectory in the plane...

 

[BvU]

sorry , for T , it should be (-w sin wt i + w coswt j ) / w
, similarly ,
for N , it should be = (-(w^2)((coswt)^2) i - (w^2)((sinwt)^2) j ) / (w^2)
Again , here's the formula have in my book

Yes, so you have $\vec T = \omega(-\sin \omega t,\cos\omega t)$ and $\vec N = -\omega^2 \vec r\ .\ \$ Easier on the eyes...

[edit] Oops! it's even simpler. See #77 for a corrected version...

------------------------------------And no need to repeat the formula in your book, that way we will end up with > 100 posts and many many pages ...

 

[BvU]

do you mean express it in form of unit vector ?

No, I mean do you know the something in $$|\vec r'\times\vec r''| = |\vec r'| \;|\vec r''|\; \text{something} $$

 

[chetzread]

No, I mean do you know the something in $$|\vec r'\times\vec r''| = |\vec r'| \;|\vec r''|\; \text{something} $$

well, here's my working...I didnt get the same ans though, which part of working is wrong?
i get w and 1 respectively when i used different approach...

 

[BvU]

If you recognize $\vec r = (cos\omega t, \sin\omega t)$ as describing the unit circle, you know which of the answers for $\kappa = {1\over \rho}$ is wrong ...
Check your own post #66...

And cry out that I made two huge mistakes in post #72 -- sorry about that !

 

[chetzread]

If you recognize $\vec r = (cos\omega t, \sin\omega t)$ as describing the unit circle, you know which of the answers for $\kappa = {1\over \rho}$ is wrong ...
Check your own post #66...

And cry out that I made two huge mistakes in post #72 -- sorry about that !

i still couldn't figure out which part is wrong, can you point out?

 

[BvU]

i still couldn't figure out which part is wrong, can you point out?

A unit circle has a radius 1, so my guess is that the answer 1 is correct and the answer $|\vec \omega|$ is wrong. And I've found why and it's somewhat my fault because in post #72 I made two huge mistakes.
Note that we are doing two things in parallel: working out the simple example $\vec r = (cos\omega t, \sin\omega t)$ and make an inroad for your long-standing question as in post #1, #13 and #63.

- - - - - - - -

I humbly fix #72:

So far we have the unit vectors () $\ \ \vec T = (-\sin \omega t,\cos\omega t)\ \$ and $\ \ \vec N = -\vec r\ \$ Curvature is 1 and radius is 1.

- - - - - - -

In the more general case the acceleration was decomposed into a tangential component by means of projection . You did not have a problem with that step ? Because we are going to use that to understand the magnitude of the normal component "The second equalities will be left as exercises"

 

[chetzread]

A unit circle has a radius 1, so my guess is that the answer 1 is correct and the answer $|\vec \omega|$ is wrong. And I've found why and it's somewhat my fault because in post #72 I made two huge mistakes.
Note that we are doing two things in parallel: working out the simple example $\vec r = (cos\omega t, \sin\omega t)$ and make an inroad for your long-standing question as in post #1, #13 and #63.

- - - - - - - -

I humbly fix #72:

So far we have the unit vectors () $\ \ \vec T = (-\sin \omega t,\cos\omega t)\ \$ and $\ \ \vec N = -\vec r\ \$ Curvature is 1 and radius is 1.

- - - - - -

In the more general case the acceleration was decomposed into a tangential
component by means of projection . You did
not have a problem with that step ? Because
we are going to use that to understand the
magnitude of the normal component "The second equalities will be left as exercises"

You mean k=(T't) /(r't) is wrong?

 

[BvU]

You mean k=(T't) /(r't) is wrong?

I don't know how to divide a vector by a vector. (or perhaps I intentionally misunderstand your notation )
Anyway, yes: that $\kappa\equiv \displaystyle {|\vec T'|\over |\vec r'|}$ evaluates to $|\omega|/ |\omega| = 1$.

 

[chetzread]

I don't know how to divide a vector by a vector. (or perhaps I intentionally misunderstand your notation )
Anyway, yes: that $\kappa\equiv \displaystyle {|\vec T'|\over |\vec r'|}$ evaluates to $|\omega|/ |omega| = 1$.

T'(t) = (omega ^2) , right?

 

[BvU]

T'(t) = (omega ^2) , right?

No, not if $\ \ \vec T = (-\sin \omega t,\cos\omega t)\ \$...

And:
Please please please become adept at using a sensible and consistent notation. $\vec T'$ is a vector. $\omega^2$ is a number. They can never never never be equal.

 

[chetzread]

No, not if $\ \ \vec T = (-\sin \omega t,\cos\omega t)\ \$...

And:
Please please please become adept at using a sensible and consistent notation. $\vec T'$ is a vector. $\omega^2$ is a number. They can never never never be equal.

$\ \ \vec T = (-w\sin \omega t, w\cos\omega t)\ \$...
$\ \ \vec T' = (-(w^2)\cos \omega t, (w^2)\sin\omega t)\ \$...
why you left out w for $\ vec T\$...
Here's my previous working

 

[BvU]

In your working (I had seen it and checked it already) in the expression for $\vec T$ you can divide out the $\omega$ in the numerator against the $\omega$ in the denominator. (That way you also get a vector that clearly has length 1). Differentiate wrt time to get $\vec T' = -\omega \;(\cos\omega t, \sin\omega t)$ ...

The expression for $\vec T$ in your working may be right (apart from the incorrect notation), but
you should still correct your expression for $\vec N$: it is not correct.

 

[chetzread]

In your working (I had seen it and checked it already) in the expression for $\vec T$ you can divide out the $\omega$ in the numerator against the $\omega$ in the denominator. (That way you also get a vector that clearly has length 1). Differentiate wrt time to get $\vec T' = -\omega \;(\cos\omega t, \sin\omega t)$ ...

The expression for $\vec T$ in your working may be right (apart from the incorrect notation), but
you should still correct your expression for $\vec N$: it is not correct.

do you mean by cancelling off the w in the denominator and numerator $\vec T$
and cancelling off (w^2) in the denominator and numerator $\vec T'$
eventually, we get magnitude of $\vec T$ and $\vec T'$ equal to 1? k =1 ?

 

[chetzread]

In your working (I had seen it and checked it already) in the expression for $\vec T$ you can divide out the $\omega$ in the numerator against the $\omega$ in the denominator. (That way you also get a vector that clearly has length 1). Differentiate wrt time to get $\vec T' = -\omega \;(\cos\omega t, \sin\omega t)$ ...

The expression for $\vec T$ in your working may be right (apart from the incorrect notation), but
you should still correct your expression for $\vec N$: it is not correct.

tat's weird, how can we do that?

 

[BvU]

do you mean by cancelling off the w in the denominator and numerator $\vec T$

yes

and cancelling off (w^2) in the denominator and numerator $\vec T'$

No. You differentiate wrt time . See post #83.

eventually, we get magnitude of $\vec T$ and $\vec T'$ equal to 1? k =1 ?

Yes for $|\vec T|$, beccause $\vec T$ is a unit vector.
No for $|\vec T'|$ because $\vec T'$ is NOT a unit vector. (but of course $\vec N \equiv \vec T'/|\vec T'|$ IS a unit vector !)

see the example. Very useful example !​

tat's weird, how can we do that?

Because $\omega$ is a scalar. Not to be confused with possible vectors $\vec \omega$.

In case you insist on a vector $\vec \omega$ in the example: there you have $\vec \omega = (0,0, \omega)$ pointing in the z direction. In short, with the scalar $\omega$, the norm of $\vec \omega$ is meant.) I agree that one can become confused, especially when sloppy or inconsistent with notation in general .​