- #1
cschear87
- 25
- 0
Homework Statement
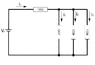
In the circuit shown in Figure Q8 below, if Vs = 10V, use Kirchoff’s Laws to determine the currents i1, i2, i3 and the source current is. Calculate the power dissipated by the resistors in this circuit. Confirm that the power dissipated by the resistors is the same as the power supplied by the power sources.
Homework Equations
kirchhoff's current law
kirchhoff's voltage law
i1=i2+i3
The Attempt at a Solution
I've genuinely tried to get the answers to this but I just don't understand it. I want to understand the answer and how the answer was reached. I have another diagram which I want to do on my own from the help given here.

 And you're very good to try and help. This course is all online with my university so I have very little interaction with other students and professors unfortunately which is why I haven't gotten an answer back about this from them. Online tutorial next week though.
And you're very good to try and help. This course is all online with my university so I have very little interaction with other students and professors unfortunately which is why I haven't gotten an answer back about this from them. Online tutorial next week though.  )
)